Định nghĩa khối lập phương
Lưu về Facebook:
Lý thuyết về Định nghĩa khối lập phương
Khối lập phương là một khối hộp gồm có
- 6 mặt đều là hình vuông
- có 12 cạnh bằng nhau
- 8 đỉnh
- cứ 3 cạnh gặp nhau tại 1 đỉnh
- có 4 đường chéo cắt nhau tại một điểm.
Khối lập phương là tập hợp những điểm nằm bên trong và các điểm nằm trên các mặt, cạnh, đỉnh này.
Bài tập tự luyện có đáp án
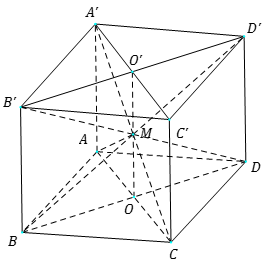
Câu 1: Cho hình lập phương $ABCD.A'B'C'D'$ và điểm $M$ thuộc miền trong của hình lập phương sao cho thể tích các khối chóp $MABC{D},\,MA'B'C'D',$ $MABB'A',$ $MCDD'C'$ bằng nhau. Khẳng định nào sau đây là đúng?
- A
- B
- C
- D

$d\left( M;\left( ABC {D} \right) \right)=d\left( M;\left( A'B'C'D' \right) \right)=d\left( M;\left( ABB'A' \right) \right)=d\left( M;C {D}D'C' \right)$
Hay $M$ là trung điểm của đoạn thẳng nối tâm hai đáy.