Định luật bảo toàn động lượng
Lưu về Facebook:
Lý thuyết về Định luật bảo toàn động lượng
+Mối quan hệ giữa động lượng pX và động năng KX của hạt X là: p2X=2mXKX
+ Khi tính vận tốc v hay động năng K thường áp dụng quy tắc hình bình hành
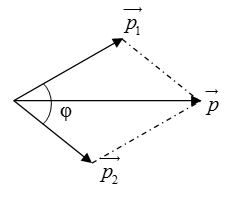
Ví dụ: →p=→p1+→p2 biết φ=^→p1,→p2
p2=p21+p22+2p1p2cosφ
hay (mv)2=(m1v1)2+(m2v2)2+2m1m2v1v2cosφ
haymK=m1K1+m2K2+2√m1m2K1K2cosφ
Tương tự khi biết φ 1=^→p1,→p hoặc φ 2=^→p2,→p
Trường hợp đặc biệt:→p1⊥→p2 Þ p2=p21+p22
Tương tự khi →p1⊥→p hoặc →p2⊥→p
+ v=0(p=0)⇒p1=p2
+ K1K2=v1v2=m2m1≈A2A1
Tương tự v1=0 hoặc v2=0.
Bài tập tự luyện có đáp án
Câu 1: Cho phản ứng hạt nhân sau 3717Cl+X→n+3718Ar . Hạt nhân X là
- A
- B
- C
- D
Phương trình phản ứng hạt nhân: 3717Cl+11X→n+3718Ar
X là 11H.