Trường hợp đồng dạng thứ nhất
Lý thuyết về Trường hợp đồng dạng thứ nhất
Trường hợp đồng dạng thứ nhất cạnh – cạnh – cạnh
Định lý:
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
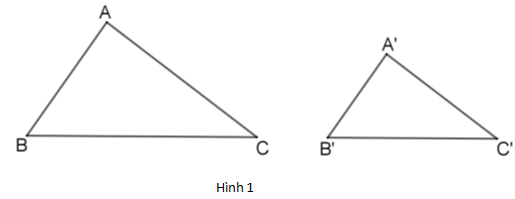
Nếu \[\Delta ABC\] và $\Delta A'B'C'$ có $\dfrac{AB}{A'B'}=\dfrac{BC}{B'C'}=\dfrac{AC}{A'C'}$ (hình 1) thì \[\Delta ABC\sim \Delta A'B'C'\left( c.c.c \right)\]
Bài tập tự luyện có đáp án
Câu 1: Cho tam giác ABC có $ AB=6,AC=7,BC=8 $ . Trên tia đối của tia AC lấy P sao cho $ \Delta ABC\sim \Delta BPC $ . Chu vi tam giác PBC bằng
- A
- B
- C
- D

$ \begin{array}{l} \Delta ABC\sim \Delta BPC\Rightarrow \dfrac{AB}{BP}=\dfrac{BC}{PC}=\dfrac{AC}{BC} \\ \Leftrightarrow \dfrac{6}{BP}=\dfrac{8}{PC}=\dfrac{7}{8}\Leftrightarrow \left\{ \begin{array}{l} BP=\dfrac{48}{7} \\ PC=\dfrac{64}{7} \end{array} \right. \end{array} $
Chu vi tam giác PBC bằng $ BP+BC+PC=24 $
Câu 2: Nếu hai tam giác $ ABC $ và $ MNP $ có $ \dfrac{AB}{NP}=\dfrac{BC}{MN}=\dfrac{CA}{MP} $ thì
- A
- B
- C
- D
$ \dfrac{AB}{NP}=\dfrac{BC}{MN}=\dfrac{CA}{MP}\Rightarrow \Delta ABC\sim \Delta PNM\Rightarrow \widehat{ABC}=\widehat{MNP} $
Câu 3: Cho tam giác ABC đường cao AH. Trên $ AH $ lấy $ H' $ . Đường thẳng qua $ H' $ và song song với $ BC $ cắt $ AB,AC $ lần lượt tại $ M,N $ . Có bao nhiêu cặp tam giác đồng dạng.
- A
- B
- C
- D

Vì $ MN//BC\Rightarrow \dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}=\dfrac{AH'}{AH} $
$ \Rightarrow \Delta AMH'\sim \Delta ABH,\Delta AH'N\sim \Delta AHC,\Delta AMN\sim \Delta ABC $
Vậy có 3 cặp tam giác đồng dạng.
Câu 4: Cho $ \Delta ABC\sim \Delta A'B'C' $ theo tỉ số $ \dfrac{1}{4} $ . Khẳng định nào dưới đây đúng?
- A
- B
- C
- D
Ta có $ \Delta ABC\sim \Delta A'B'C' $ theo tỉ số $ \dfrac{1}{4} $ nên
$ \dfrac{AB}{A'B'}=\dfrac{AC}{A'C'}=\dfrac{BC}{B'C'}=\dfrac{1}{4} $ .
Câu 5: Cho hai tam giác như hình vẽ. Khẳng định nào sau đây là đúng? 
- A
- B
- C
- D
Câu 6: Cho $ \Delta ABC\sim \Delta A'B'C' $ theo tỉ số đồng dạng $ k $ . Có bao nhiêu khẳng định đúng trong các khẳng định sau. A. $ \dfrac{AB}{A'B'}=\dfrac{AC}{B'C'} $
B. $ AB=k\text{A}'B' $
C. $ AC.B'C'=BC.A'C' $
D. $ A'B'=kAB $
A. $ \dfrac{AB}{A'B'}=\dfrac{AC}{B'C'} $
B. $ AB=k\text{A}'B' $
C. $ AC.B'C'=BC.A'C' $
D. $ A'B'=kAB $
- A
- B
- C
- D
Vì $ \Delta ABC\sim \Delta A'B'C' $ nên ta có
$ \dfrac{AB}{A'B'}=\dfrac{AC}{A'C'}=\dfrac{BC}{B'C'}=k $
Vậy Khẳng định B và C là đúng.
Xem thêm các bài tiếp theo bên dưới