Xét các số thực dương phân biệt x, y thỏa mãn $\large \dfrac{x+y}{x-y}

Xét các số thực dương phân biệt x, y thỏa mãn $\large \dfrac{x+y}{x-y}=\log_2 3.$ Khi biểu thức $\large 4^{x+y}+16.3^{y-x}$ đạt giá trị nhỏ nhất, giá trị của x + 3y bằng

• A.

  A. $\large 2-\log_23$

• B.

  B. $\large 1+\log_32$

• C.

  C. $\large 2-\log_32$

• D.

  D. $\large 1+\log_23$

Ta có:

$\large \dfrac{x+y}{x-y}=\log_23\Leftrightarrow y-x=-(x+y)\log_32\Leftrightarrow 3^{y-x}=3^{-(x+y)\log_32}\Leftrightarrow 3^{y-x}=\dfrac{1}{2^{x+y}}$

Đặt $\large P=4^{x+y}+16.3^{y-x}=4^{x+y}+\dfrac{16}{2^{x+y}}$

Đặt: $\large t=2^{x+y}, t>1$. Khi đó: $\large P=t^2+\dfrac{16}{t}, P'=2t-\dfrac{16}{t^2}; P'=0\Leftrightarrow t=2$

Bảng biến thiên: 

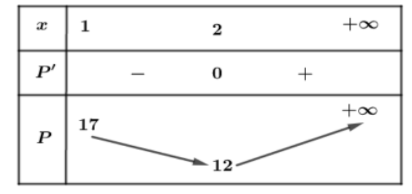
Dựa vào bảng biến thiên ta thấy $\large \underset{(1; +\infty)}{Min} P=12\Leftrightarrow t=2\Leftrightarrow x+y=1 (1)$

Thay (1) vào $\large \dfrac{x+y}{x-y}=\log_23$ ta được $\large x-y=\log_32 (2)$

Từ (1) và (2) suy ra $\large \left\{\begin{align}& x=\dfrac{1}{2}+\dfrac{1}{2}.\log_32\\& y=\dfrac{1}{2}-\dfrac{1}{2}.\log_32\\\end{align}\right.$. Do đó: $\large x+3y=2-\log_32$