Cho hàm số $\large f(x)=ax^4+bx^3+cx^2+dx+e, (ae 0$ Vậy hàm số có 3 đi

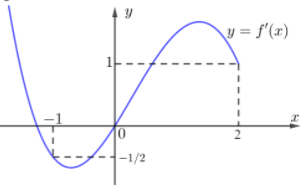
Cho hàm số $\large f(x)=ax^4+bx^3+cx^2+dx+e, (ae<0)$. Đồ thị hàm số $\large y=f'(x)$ như bên. Hàm số $\large y=\left| 4f(x)-x^2\right| $ có bao nhiêu điểm cực tiểu?

• A. A. 2
• B. B. 3
• C. C. 5
• D. D. 4

Xét hàm số $\large h(x)=f(x)-\dfrac{x^2}{4}\Rightarrow h'(x)=f'(x)-\dfrac{x}{2}$

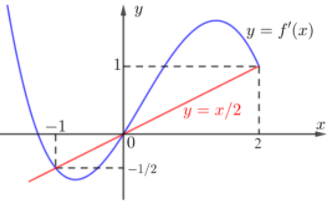
Từ đồ thị và giả thiết ta có $\large \Rightarrow h'(x)=4a(x+1)x(x+2), (a<0)$

Do $\large ae<0\Rightarrow e>0\Leftrightarrow f(0)>0\Leftrightarrow h(0)>0$

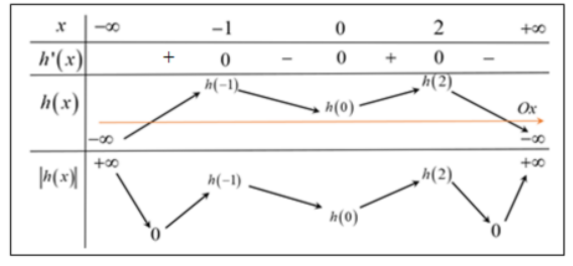
Vậy hàm số có 3 điểm cực tiểu.