Trong thí nghiệm giao thoa sóng nước, hai nguồn sóng S1 và $

MỤC LỤC
Câu hỏi:
Trong thí nghiệm giao thoa sóng nước, hai nguồn sóng S1 và S2 cách nhau 11cm dao động theo phương vuông góc với mặt nước với cùng phương trình u1=u2=5cos(100πt)(mm) .Tốc độ truyền sóng v = 0,5m/s và biên độ sóng không đổi trong quá trình truyền đi. Chọn hệ trục xOy thuộc mặt phẳng mặt nước khi yên lặng, gốc O trùng với S1,Ox trùng với S1S2. Trong không gian, phía trên mặt nước có một chất điểm chuyển động mà hình chiếu P của nó tới mặt nước chuyển động với phương trình quỹ đạo y=x+2 và có tốc độ v1=5√2cm/s . Trong thời gian t = 2s kể từ lúc P có tọa độ xp=0 thì P cắt bao nhiêu vẫn cực đại trong vùng giao thoa sóng?
Đáp án án đúng là: C
Lời giải chi tiết:
Phương pháp:
Công thức bước sóng: λ=v.T=v.2πω
Điều kiện để có cực đại giao thoa là: d1−d2=kλ;k∈Z
Lời giải:
Bước sóng: λ=vT=v.2πω=50.2π100π=1cm
Trên đoạn nối hai nguồn có số cực đại là số giá trị k thỏa mãn:
$\large -\dfrac{S_1S_2}{\lambda}
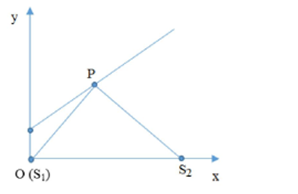
Khi xp=0 ta có {S1P=2S2P=√S1S22+OP2=√112+22=5√5cm
Vậy ta có: S2P−S1P=5√5−2=9,18=9,18λ
Tức là P ban đầu nằm ngoài cực đại bậc 9.
P chuyển động với vận tốc vì, sau thời gian 2 giây thì quãng đường nó đi được là:
S=v1t=5√2.2=10√2cm=√x2+(y−2)2=√x2+(x+2−x)2
⇒x=10⇒y=12
Tọa độ của điểm P lúc đó là (10; 12); tức là x = 10cm; y = 12cm.
Ta có:
{S1Pt=√x2+y2=2√61S2Pt=√(11−x)2+y2=√145 S2Pt−S1Pt=−3,57.−3,57λ
Vậy lúc này P nằm ngoài cực đại bậc 3.
Tổng số vận cực đại mà P đã cắt là các vấn có: k = 9;8;7;...0;-1;-2;-3
Tổng cộng là 13 vân.
Chọn C.
Xem thêm các bài tiếp theo bên dưới
- Một mạch điện xoay chiều RLC nối tiếp có: $\large R=100\Omega; C=\dfra
- Trên một sợi dây đang có sóng dừng. Sóng truyền trên sợi dây có bước s
- Giới hạn quang điện của kẽm là λ0=0,35μm . Công tho
- Vật sáng AB vuông góc với trục chính của thấu kính cho ảnh ngược chiều
- Tiến hành thí nghiệm với 2 con lắc lò xo A và B có quả nặng và chiều d