Trong hiện tượng giao thoa sóng nước, hai nguồn A, B cách nhau 10 cm d

Trong hiện tượng giao thoa sóng nước, hai nguồn A, B cách nhau 10 cm dao động cùng biên độ, cùng pha, tạo ra sóng cơ có bước sóng 4 cm. C là điểm trên mặt nước sao cho ABC là tam giác vuông tại C với BC = 8 cm. M và N là hai cực đại giao thoa trên BC gần nhau nhất. Độ dài đoạn MN có giá trị gần nhất với giá trị nào sau đây? 

• A. 2,4 cm.
• B. 2,8 cm.
• C. 1,3 cm.
• D. 1,9 cm.

Phương pháp: 
Điều kiện cực đại giao thoa: $\Large d_2-d_1=k\lambda$
Điều kiện cực tiểu giao thoa: $\Large d_2-d_1=\left(k+\dfrac{1}{2}\right)\lambda$
Sử dụng máy tính bỏ túi để giải nghiệm phương trình 
Cách giải: 
 
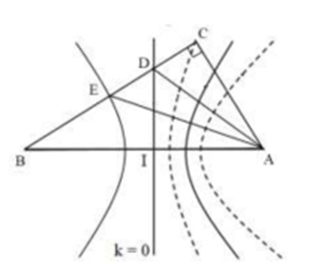
Ta có: $\Large AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{10^{2}-8^{2}}=6(cm)$  
Tại điểm C có: $\Large BC-AC=2(cm)=\dfrac{\lambda}{2}\rightarrow$ điểm C thuộc đường cực tiểu bậc 1 
$\Large \rightarrow$ Để trên CB có 2 điểm cực đại gần nhau nhất, D và E thuộc đường cực đại bậc 0 và bậc 1 (như hình vẽ) 
D nằm trên cực đại bậc 0, ta có: 
$\Large DA=DB=x\Rightarrow x+\sqrt{x^{2}-6^{2}}=8\Rightarrow x=6,25(cm)$
Điểm E nằm trên cực đại bậc 1, ta có:  $\Large EA-EB=\lambda\Rightarrow EA=EB+\lambda$
Đặt $\Large EB=y\Rightarrow EA=y+4$
$\Large \Rightarrow y+\sqrt{(y+4)^{2}-6^{2}}\Rightarrow y=3,5(cm)$
 $\Large \Rightarrow DE=x-y=6,25-3,5=2,75(cm)$
Giá trị tìm được gần nhất với giá trị 2,8 cm