Đặt điện áp $\Large u=220\sqrt{2}\cos\left(100\pi t-\dfrac{\pi}{4}\rig

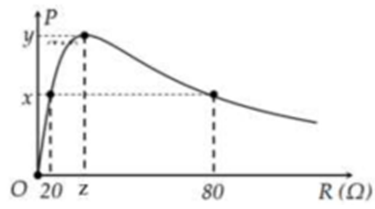
Đặt điện áp $\Large u=220\sqrt{2}\cos\left(100\pi t-\dfrac{\pi}{4}\right)(V)$ vào hai đầu đoạn mạch gồm: biến trở R, cuộn cảm thuần L và tụ điện C người ta thu được đồ thị biểu diễn quan hệ giữa công suất mạch điện với điện trở R như hình vẽ. Giá trị x, y, z lần lượt là

• A. 400; 500; 40.
• B. 484; 1210; 40.
• C. 484; 605; 40.
• D. 484; 40; 605.

Phương pháp: 
Công suất của đoạn mạch điện xoay chiều: $\Large P=\dfrac{U^{2}R}{R^{2}+(Z_L-Z_C)^{2}}$ 
Khi R thay đổi, công suất trong mạch đạt cực đại khi: $\Large R=|Z_L-Z_C|$ 
Định lí Vi- et cho phương trình $\Large ax^{2}+bx+c=0$: $\Large \left\{\begin{align}&x_1x_2=\dfrac{c}{a}\\&x_1+x_2=-\dfrac{b}{a}\\\end{align}\right.$
Cách giải: 
Công suất của mạch điện là: 
 $\Large P=\dfrac{U^{2}R}{R^{2}}+(Z_L-Z_C)^{2}\Rightarrow PR^{2}-U^{2}R+P(Z_L-Z_C)^{2}=0(1)$
Khi $\Large R=20\Omega$ và $\Large R=80\Omega$ mạch có cùng công suất. 
Áp dụng định lí Vi- et cho phương trình (1) với ẩn là R, ta có: 
 $\Large \left\{\begin{align}&R_1R_2=(Z_L-Z_C)^{2}=20.80=160\\&R_1+R_2=\dfrac{U^{2}}{P}\Rightarrow 20+80=\dfrac{220^{2}}{P}\Rightarrow P=x=484(W)\\\end{align}\right.$
Công suất trong mạch đạt cực đại khi: 
 $\Large R=|Z_L-Z_C|=\sqrt{1600}=40(\Omega)\Rightarrow z=40(\Omega)$
Khi đó, công suất cực đại của mạch là: 
 $\Large P_{max}=\dfrac{U^{2}R}{2R^{2}}=\dfrac{220^{2}.40}{2.40^{2}}=605(W)\Rightarrow y=605(W)$