Tính thể tích của khối trụ biết chu vi đáy của hình trụ đó bằng $\larg
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Tính thể tích của khối trụ biết chu vi đáy của hình trụ đó bằng 6π (cm) và thiết diện đi qua trục là một hình chữ nhật có độ dài đường chéo bằng 10 (cm).
Đáp án án đúng là: C
Lời giải chi tiết:
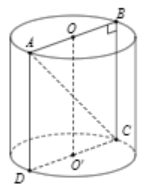
Gọi O, O’ là hai tâm của đáy hình trụ và thiết diện qua trục là hình chữ nhật ABCD. Do chu vi đáy của hình trụ đó bằng 6π (cm) nên bán kính đáy của hình trụ là R=C2π=6π2π=3(cm)
Vì thiết diện đi qua trục là một hình chữ nhật ABCD có AC = 10 (cm) và AB = 2R = 6 (cm) nên chiều cao của hình trụ là:
h=OO′=BC=√AC2−AB2=√102−62=8 (cm).
Vậy thể tích khối trụ là: V=πR2h=π.32.⇒=72π (cm3)
Xem thêm các bài tiếp theo bên dưới
- Cho hình nón có bán kính đáy bằng a , độ dài đường sinh bằng 2 a . Góc
- Cho mặt cầu S(O;R) và một điểm A , biết OA = 2R . Qua A kẻ một tiếp tu
- Xét các mệnh đề (I) Tập hợp các đường thẳng d thay đổi nhưng luôn luôn
- Một tấm nhôm hình chữ nhật có hai kích thước là a và 2 a ( a là độ dài
- Cho hình nón đỉnh S có đáy là hình tròn tâm O , bán kính R . Dựng hai