Tìm tất cả các giá trị thực của tham số $\Large m$ để phương trình sau

Tìm tất cả các giá trị thực của tham số $\Large m$ để phương trình sau có hai nghiệm thực phân biệt:

$\Large x \log_{3}(x + 1) = \log_{9}\left [ 9(x+1)^{2m} \right ]$

• A.

  A. $\Large m \in (-1; 0)$

• B.

  B. $\Large m \in (-1; +\infty )$

• C.

  C. $\Large m \in (-2; 0)$

• D.

  D. $\Large m \in [-1; 0)$

Chọn B

Phương trình 

$\Large \Leftrightarrow x \log_{3}(x + 1) = 1 + m \log_{3}(x+1)$

$\Large \Leftrightarrow m = x - \dfrac{1}{\log_{3}(x + 1)}$ với $\Large \left\{\begin{array}{l}x > -1 \\x \neq 0 \\\end{array}\right.$

Xét hàm số $\Large f(x) = x - \dfrac{1}{\log_{3}(x + 1)}$ với $\Large \left\{\begin{array}{l}x > -1 \\x \neq 0 \\\end{array}\right.$

$\Large f{}'(x) = 1 + \dfrac{1}{(x+1) \ln 3 .\log_{3}^{2}(x + 1)} > 0$ với mọi $\Large \left\{\begin{array}{l}x > -1 \\x \neq 0 \\\end{array}\right.$

Bảng biến thiên

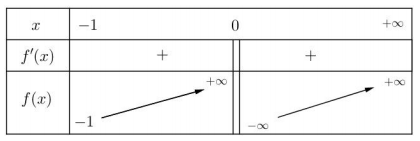
Dựa vào bảng biến thiên để phương trình có hai nghiệm thì $\Large m \in (-1; +\infty )$.