Gọi $\Large (C) $ là đồ thị hàm số $\Large y = \dfrac{x -7}{x + 1}$, $

Gọi $\Large (C) $ là đồ thị hàm số $\Large y = \dfrac{x -7}{x + 1}$, $\Large A, B$ là các điểm thuộc $\Large (C) $ có hoành độ lần lượt là 0 và 3. $\Large M $ là điểm thay đổi trên $\Large (C) $ sao cho $\Large 0 < x_{M} < 3$. Tìm giá trị lớn nhất của diện tích tam giác $\Large ABM$.

• A.

  A. $\Large 6$

• B.

  B. $\Large3\sqrt{5}$

• C.

  C. $\Large 3$

• D.

  D. $\Large 5$

Chọn C

Ta có: $\Large S_{\Delta ABM} = \dfrac{1}{2}AB. d\left ( M; AB \right )$

Theo đề bài ta có $\Large A(0;-7)$; $\Large B(3;-1)$, $\Large M\left ( x_{M};\dfrac{x_{M} - 7}{x_{M} + 1} \right )$.

Phương trình đường thẳng $\Large AB$:

$\Large \dfrac{x - 0}{3 - 0} = \dfrac{y + 7}{-1 + 7}$

$\Large \Leftrightarrow \dfrac{x }{3 } = \dfrac{y + 7}{6}$

$\Large \Leftrightarrow 2x = y + 7$

$\Large \Leftrightarrow 2x - y - 7 = 0$

Ta có:

$\Large d(M; AB) = \dfrac{\left | 2x_{M} - \dfrac{x_{M}-7}{x_{M}+1} - 7\right |}{\sqrt{4 + 1}}= \dfrac{\left | \dfrac{2x_{M}^{2} - 6x_{M}}{x_{M}+ 1} \right |}{\sqrt{5}}$

$\Large S_{\Delta ABM} = \dfrac{1}{2}\sqrt{45}.\dfrac{\left | \dfrac{2x_{M}^{2} - 6x_{M}}{x_{M} + 1} \right |}{\sqrt{5}} = \dfrac{3}{2}\left | \dfrac{2x_{M}^{2} - 6x_{M}}{x_{M} + 1} \right |$

Xét hàm số $\Large f(t) = \dfrac{2t^{2} - 6t}{t + 1}$ trên (0;3), có:

$\Large f{}'(t) = \dfrac{2t^{2} + 4t - 6}{(t + 1)^{2}}$

$\Large f{}'(t) = 0 \Leftrightarrow \left[\begin{array}{l}t = 1 \\t = -3 \\\end{array}\right.$

$\Large f(1) = -2; f(0) = 0; f(3) = 0$

Bảng biến thiên

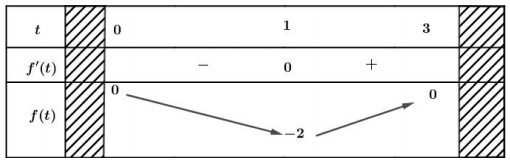
Dựa vào bảng biến thiên, ta có $\Large \left | f(t) \right |$, đạt giá trị lớn nhất bằng $\Large \left | f(1) \right | = 2$. Vậy $\Large \Delta ABM$ có diện tích lớn nhất bằng $\Large \dfrac{3}{2}.2 = 3$.