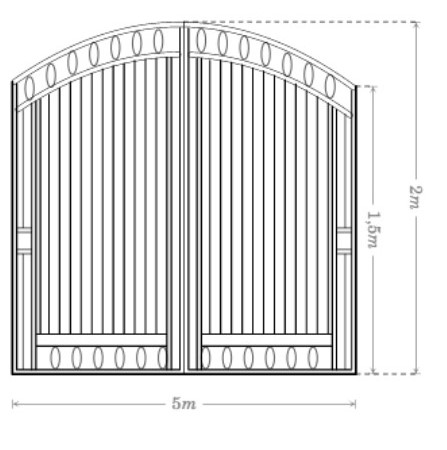
Ông An muốn làm cửa rào sắt có hình dạng và kích thước như hình vẽ bên

Ông An muốn làm cửa rào sắt có hình dạng và kích thước như hình vẽ bên , biết đường cong phía trên là một Parabol . Giá $\Large 1{{m}^{2}}$ của rào sắt là 700.000 đồng . Hỏi ông An phải trả bao nhiêu tiền để làm cái cửa sắt như vậy (làm tròn đến hàng nghìn)

• A.

  A. 6.620.000 đồng 

• B.

  B. 6.320.000 đồng 

• C.

  C. 6.520.000 đồng

• D.

  D. 6.417.000 đồng

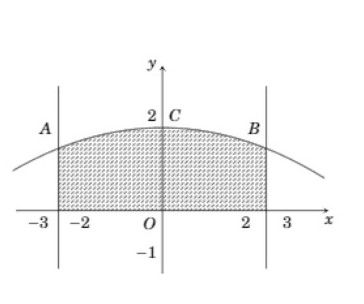
Ta chọn hệ trục tọa độ như hình vẽ 

Trong đó $\Large A(-2,5;1,5),B(2,5;1,5),C(0;2)$ 

Giả sử đường cong phía trên là một Parabol có dạng $\Large y=a{{x}^{2}}+bx+c$ , với $\Large a,b,c\in R$

Do Parabol đi qua điểm $\Large A(-2,5;1,5),B(2,5;1,5),C(0;2)$ nên ta có hệ phương trình 

$\Large \left\{ \begin{align}  & a{{(-2,5)}^{2}}+b(-2,5)+c=1,5 \\\Large   & a{{(2,5)}^{2}}+b(2,5)+c=1,5 \\ \Large  & c=2 \\ \end{align} \right.$ $\Large \Leftrightarrow \left\{ \begin{align}  & a=-\frac{2}{25} \\ \Large  & b=0 \\  \Large & c=2 \\ \end{align} \right.$

Khi đó phương trình Parabol là $\Large y=-\frac{2}{25}{{x}^{2}}+2$

Diện tích $\Large S$ của cửa rào sắt là diện tích phần hình phẳng giới hạn bởi đồ thị hàm số $\Large y=-\frac{2}{25}{{x}^{2}}+2$ , trục hoành và hai đường thẳng $\Large x=-2,5;x=2,5$

Ta có: $\Large S=\int\limits_{-2,5}^{2,5}{\left( -\frac{2}{25}{{x}^{2}}+2 \right)dx=\left( -\frac{2}{25}.\frac{{{x}^{3}}}{3}+2x \right)\left| \begin{align}  & 2,5 \\ \Large  & -2,5 \\ \end{align} \right.=\frac{55}{6}}$

Vậy ông An phải trả số tiền để làm cái cửa sắt là $\Large S.700000=\frac{55}{6}.700000\approx 6.417.000$ (đồng)

Chọn đáp án D