Một vật đang dao động điều hòa, gọi $\large t_{1}, t_{2}$ và $t_{3}$ l

MỤC LỤC
Câu hỏi:
Một vật đang dao động điều hòa, gọi $\large t_{1}, t_{2}$ và $t_{3}$ lần lượt là ba thời điểm liên tiếp vật có cùng tốc độ. Biết rằng $\large t_{3} – t_{1} = 3(t_{3}- t_{2}) = 0,1s$ và $\large v_{1} = v_{2} = - v_{3} = 20\pi cm/s$. Biên độ dao động của vật là
Đáp án án đúng là: A
Lời giải chi tiết:
Ở thời điểm $\large t_{1}$ và $\large t_{3}$ vận tốc vật trái dấu nhau => hai vị trí này đối xứng nhau qua gốc tọa độ => $\large {{\varphi }_{13}}$= π
Mặt khác $\large t_{3} – t_{1} = 3(t_{3} – t_{2})$
=> $\large {{\varphi }_{13}}$ = 3${{\varphi }_{32}}$=> $\large {{\varphi }_{32}}= \dfrac{\pi }{6}$
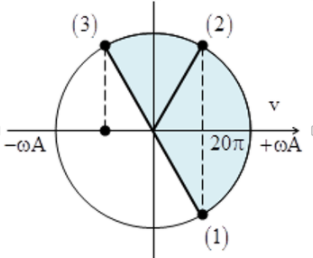
Từ hình vẽ ta có
$\large sin \dfrac{{{\varphi }_{32}}}{2}=\dfrac{10\pi }{\omega A}\Rightarrow \omega A=20\pi cm/s$
$\large {{t}_{13}}=\dfrac{{{\varphi }_{13}}}{\omega }=0,1s\Rightarrow \omega =10\pi (rad/s)\Rightarrow A=2cm$
Xem thêm các bài tiếp theo bên dưới
- Một hệ dao động có tần số dao động riêng $f_{0} = 5 Hz$. Hệ da
- Một con lắc lò xo nằm ngang dao động theo phương trình $\large x=5cos
- Một vật dao động điều hoà với phương trình $\large x=4cos (4\pi t+\dfr
- Con lắc lò xo treo thẳng đứng gồm lò xo có độ cứng k = 100 N/m và vật
- Con lắc lò xo thực hiện 100 dao động hết 10π s. Chọn gốc thời gian là