Con lắc lò xo treo thẳng đứng gồm lò xo có độ cứng k = 100 N/m và vật

MỤC LỤC
Câu hỏi:
Con lắc lò xo treo thẳng đứng gồm lò xo có độ cứng k = 100 N/m và vật nặng có khối lượng 100 g. Kéo vật nặng theo phương thẳng đứng xuống dưới làm lò xo giãn 3 cm rồi truyền cho vật vận tốc $\large 20\pi \sqrt{3}$cm/s hướng lên. Chọn trục tọa độ thẳng đứng hướng xuống, gốc tọa độ tại vị trí cân bằng, gốc thời gian là lúc truyền vận tốc. Lấy $\large g={{\pi }^{2}} m/s^{2}$, quãng đường vật đi được trong một phần ba chu kì kể từ thời điểm t = 0 là
Đáp án án đúng là: A
Lời giải chi tiết:
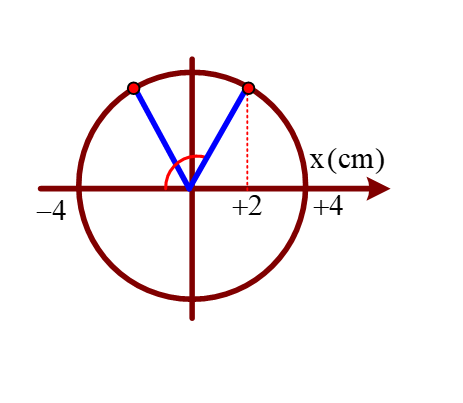
+ Độ biến dạng của lò xo tại vị trí cân bằng :
$\large \Delta {{l}_{0}}=\frac{mg}{k}=\frac{{{100.10}^{-3}}.10}{100}=1$cm.
+ Tần số góc của dao động :
$\large \omega =\sqrt{\frac{k}{m}}=\sqrt{\frac{100}{{{100.10}^{-3}}}}=10\pi $rad/s.
Kéo vật nặng theo phương thẳng đứng xuống dưới làm lò xo giãn 3 cm →
$\large x_{0} = 3 cm$ (chọn trục tọa độ với chiều dương hướng xuống).
+ Biên độ dao động của vật
$\large A=\sqrt{x_{0}^{2}+{{\left( \frac{{{v}_{0}}}{\omega } \right)}^{2}}}=\sqrt{{{2}^{2}}+{{\left( \frac{20\pi \sqrt{3}}{10\pi } \right)}^{2}}}=4$cm.
→ Từ hình vẽ ta thấy rằng, quãng đường vật đi được tương ứng sẽ là 6 cm
Xem thêm các bài tiếp theo bên dưới
- Con lắc lò xo thực hiện 100 dao động hết 10π s. Chọn gốc thời gian là
- Một chất điểm dao động điều hòa theo phương trình: $\large x=5\cos (\p
- Một vật nhỏ dao động điều hoà trên trục Ox với phương trình $\large x=
- Một con lắc lò xo gồm lò xo có chiều dài tự nhiên $l_{0} = 30 cm$. Kíc
- Một vật có khối lượng m = 100 g dao động điều hoà theo phương trình có