Một vật có khối lượng m = 100 g dao động điều hoà theo phương trình có
MỤC LỤC
Câu hỏi:
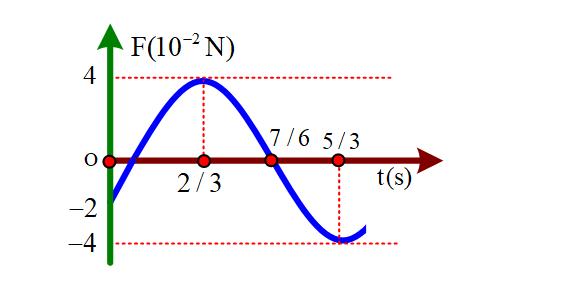
Một vật có khối lượng m = 100 g dao động điều hoà theo phương trình có dạng $\large x=A\cos (\omega t+\varphi )$ Biết đồ thị lực kéo về F(t) biến thiên theo thời gian như hình vẽ. Lấy ${\pi }^{2} = 10$. Phương trình dao động của vật là

Đáp án án đúng là: C
Lời giải chi tiết:
+ Ta có: $\large F=-kx$
+ Chu kì $\large T=2.\left( \dfrac{5}{3}-\dfrac{2}{3} \right)=2s\Rightarrow \omega =\dfrac{2\pi }{T}=\pi \left( \dfrac{rad}{s} \right)$
+ Mà $\large \omega =\sqrt{\dfrac{k}{m}}\Rightarrow k=m{{\omega }^{2}}=0,1.{{\pi }^{2}}=1\left( N/m \right)$
+ Nhìn vào đồ thị ta thấy:
${{F}_{\max }}=kA={{4.10}^{-2}}N\Rightarrow A={{4.10}^{-2}}m=4cm$
Nhìn vào đồ thị ta thấy Fmax = kA = 4.10-2N --> A = 4.10-2m = 4cm
Thời điểm t = 0 thì F = -2.10-2N và đang tăng nên x = 2cm và đang giảm. Vậy pha ban đầu $\varphi =\dfrac{\pi }{3}$.
Phương trình dao động của vật: $x=4\cos \left( \pi t+\dfrac{\pi }{3} \right)cm$
Xem thêm các bài tiếp theo bên dưới
- Một vật thực hiện đồng thời hai dao động điều hòa cùng phương cùng tần
- Vật dao động điều hòa có vận tốc cực đại bằng 3m/s và gia tốc cực đại
- Một vật dao động điều hòa dọc theo trục Ox, gọi Δt là khoảng thời gian
- Hai con lắc lò xo M và N giống hệt nhau, đầu trên của hai lò xo được c
- Hình vẽ bên là đồ thị biễu diễn sự phụ thuộc của li độ x vào thời gian