Hình vẽ bên là đồ thị biễu diễn sự phụ thuộc của li độ x vào thời gian
MỤC LỤC
Câu hỏi:
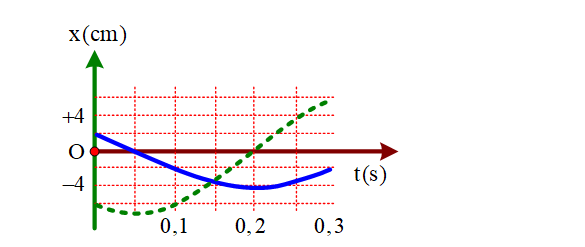
Hình vẽ bên là đồ thị biễu diễn sự phụ thuộc của li độ x vào thời gian t của hai dao động điều hòa cùng phương. Dao động của vật là tổng hợp của hai dao động nói trên. Trong 0,20 s đầu tiên kể từ t = 0, tốc độ trung bình của vật bằng.

Đáp án án đúng là: B
Lời giải chi tiết:
Từ đồ thị, ta thấy rằng dao động thành phần ứng với đường liền nét có phương trình ${{x}_{1}}=4\cos \left( \frac{10\pi }{3}t+\frac{\pi }{3} \right)$cm.
+ Thành phần dao động ứng với đường nét đứt. Tại $t=\frac{T}{12}=0,05$ s đồ thị đi qua vị trí x = –A → tại t = 0, thành phần dao động này đi qua vị trí $x=-\frac{\sqrt{3}}{2}A=-6$cm
→ $A=4\sqrt{3}$cm.
→ ${{x}_{2}}=4\sqrt{3}\cos \left( \frac{10\pi }{3}t+\frac{5\pi }{6} \right)$.cm
→ $x = x_{1} + x_{2} = 8\cos \left( \frac{10\pi }{3}t+\frac{2\pi }{3} \right)$cm.
+ Tại t = 0, vật đi qua vị trí x = –4 cm theo chiều âm. Sau khoảng thời gian Δt = 0,2 s ứng với góc quét $\Delta \varphi =\omega \Delta t={{120}^{o}}$vật đến vị trí x = –4 cm theo chiều dương.
→ ${{v}_{tb}}=\frac{4+4}{0,2}=40$cm/s.
Xem thêm các bài tiếp theo bên dưới
- Một chất điểm đang dao động điều hòa dọc theo trục Ox, mốc tính thế nă
- Một học sinh dùng đồng hồ bấm giây để đo chu kì dao động điều hòa của
- Cho hai dao động điều hòa cùng phương với các phương trình lần lượt là
- Một con lắc lò xo thẳng đứng gồm lò xo nhẹ có độ cứng k = 25 N/m một đ
- Trên mặt phẳng nằm ngang nhẵn, có một con lắc lò xo gồm lò xo có độ cứ