Một chất điểm đang dao động điều hòa dọc theo trục Ox, mốc tính thế nă

MỤC LỤC
Câu hỏi:
Một chất điểm đang dao động điều hòa dọc theo trục Ox, mốc tính thế năng tại vị trí cân bằng O. Từ thời điểm $t_{1} = 0$ đến thời điểm $t_{2}$ quả cầu của con lắc đi được một quãng đường S và chưa đổi chiều chuyển động, đồng thời động năng của con lắc giảm từ giá trị cực đại về 0,096 J. Từ thời điểm $t_{2}$ đến thời điểm $t_{3}$, chất điểm đi thêm một đoạn đường bằng 2S nữa mà chưa đổi chiều chuyển động và động năng của con lắc vào thời điểm $t_{3}$ bằng 0,064 J. Từ thời điểm $t_{3}$ đến $t_{4}$, chất điểm đi thêm một đoạn đường bằng 4S nữa thì động năng của chất điểm vào thời điểm $t_{4}$ bằng
Đáp án án đúng là: B
Lời giải chi tiết:
|
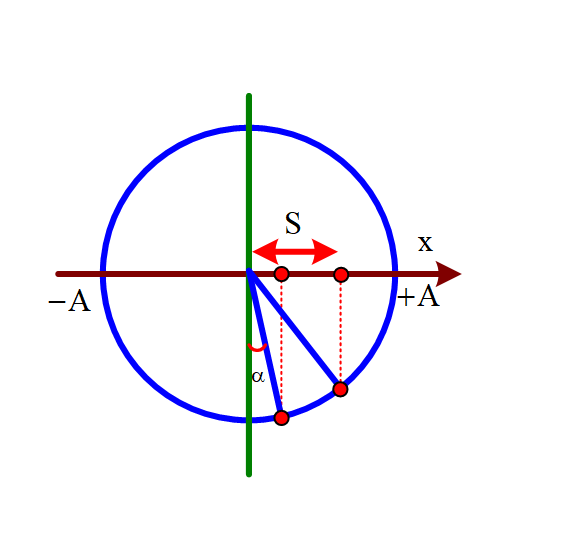
+ Biểu diễn dao động của vật tương tứng trên đường tròn Ta có: $\left\{ \begin{align}& \sin \alpha =\frac{S}{A} \\ & \sin\beta =\frac{3S}{A} \\ \end{align} \right.$=> $\left\{ \begin{align}& {{\cos }^{2}}\alpha =1-\frac{{{S}^{2}}}{{{A}^{2}}} \\ & {{\cos }^{2}}\beta =1-9.\frac{{{S}^{2}}}{{{A}^{2}}} \\ \end{align} \right.$ Với ${{\cos }^{2}}\alpha =\frac{{{E}_{d}}}{E}\Rightarrow \left\{ \begin{align}& 1\frac{{{S}^{2}}}{{{A}^{2}}}=\frac{0,096}{E} \\ & 1-9.\frac{{{S}^{2}}}{{{A}^{2}}}=\frac{0,064}{E} \\ \end{align} \right.\Rightarrow $ Lập tỉ số → S = 0,2A |
|
+ Từ thời điểm t3 vật đi thêm 4S nữa thì vật quay lại vị trí cùng li độ với điểm t3 → Eđ = 0,064
Xem thêm các bài tiếp theo bên dưới
- Một học sinh dùng đồng hồ bấm giây để đo chu kì dao động điều hòa của
- Cho hai dao động điều hòa cùng phương với các phương trình lần lượt là
- Một con lắc lò xo thẳng đứng gồm lò xo nhẹ có độ cứng k = 25 N/m một đ
- Trên mặt phẳng nằm ngang nhẵn, có một con lắc lò xo gồm lò xo có độ cứ
- Đặt điện áp $\Large\ u={{U}_{0}}\cos \omega t$vào hai đầu một mạch điệ