Một mạch dao dộng LC lí tưởng gồm cuộn cảm thuần L=2mH và tụ điện C=8p

MỤC LỤC
Câu hỏi:
Một mạch dao dộng LC lí tưởng gồm cuộn cảm thuần L=2mH và tụ điện C=8pF. Lấy $\pi ^2$=10. Thời gian ngắn nhất từ lúc tụ bắt đầu phóng điện đến lúc năng lượng điện trường bằng ba lần năng lượng từ trường là?
Đáp án án đúng là: A
Lời giải chi tiết:
Đáp án A
Phương pháp: sử dụng vòng tròn lượng giác
Cách giải:
Chu kỳ:$T=2\pi \sqrt{LC}={{8.10}^{-7}}$s
Tụ bắt đầu phóng điện: q=|$Q_o$|
Năng lượng điện trường bằng ba lần năng lượng từ trường:$q=\left| \frac{{{Q}_{o}}\sqrt{3}}{2} \right|$
Biểu thức đường tròn lượng giác ta có:
Thời gian ngắn nhất từ lúc tụ bắt đầu phóng điện đến lúc năng lượng điện trường bằng ba lần năng lượng từ trường là:$Q_o$ đến q=$\large\frac{{{Q}_{o}}\sqrt{3}}{2}$tương ứng với góc quét
$\large\alpha =\frac{\pi }{6}\Rightarrow \Delta t=\frac{\alpha }{\omega }=\alpha .\frac{T}{2\pi }=\frac{T}{12}=\frac{{{10}^{-6}}}{15}s$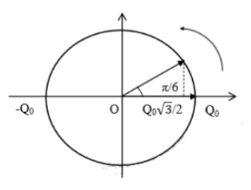
Xem thêm các bài tiếp theo bên dưới
- Một mạch dao động điện từ LC, điện tích cực đại trên tụ là $10^-6$s và
- Điện tích trong mạch LC dao động điều hòa bới chu kỳ T=$\Large 10^{-6}
- Một mạch dao động LC đang có dao động điện từ tự do. Hiệu điện thế cực
- Trong mạch dao động L có dao động điện từ tự do với điện tích cực đại
- Trong mạch dao động LC lí tưởng đang có dao động điên từ tự do với tần