Một đám nguyên tử hiđrô đang ở trạng thái cơ bản. Khi chiếu bức xạ có

Một đám nguyên tử hiđrô đang ở trạng thái cơ bản. Khi chiếu bức xạ có tần số $\large f_1$ vào đám nguyên tử này thì chúng phát ra tối đa 3 bức xạ. Khi chiếu bức xạ có tần số $\large f_2$ vào đám nguyên tử này thì chúng phát ra tối đa 10 bức xạ. Biết năng lượng ứng với các trạng thái dừng của nguyên tử hiđrô được tính theo biểu thức $\large {{\text{E}}_{\text{n}}}=-\dfrac{{{\text{E}}_{0}}}{{{\text{n}}^{2}}}$  ($\large E_0$ là hằng số dương, n = 1,2,3,…). Tỉ số $\large \dfrac{{{\text{f}}_{1}}}{{{\text{f}}_{2}}}$ là

• A. $\large \dfrac{10}{3}$.
• B. $\large \dfrac{27}{25}$.
• C. $\large \dfrac{3}{10}$.
• D. $\large \dfrac{25}{27}$ .

Đáp án D

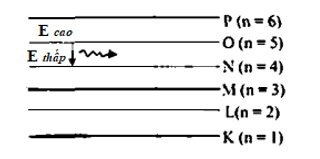
*Nguyên tử ở trạng thái  có mức năng lượng cao khi chuyển về mức năng lượng thấp ( năng lượng thấp nhất là ở trạng thái cơ bản) thì chúng phát tối đa số bức xạ:  
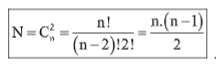  (Với n là số  quỹ đạo ).
*Chiếu $\large f_1$ đối  với đám nguyên tử thứ nhất thì số quỹ đạo tương ứng:
$\large  3=\dfrac{{{n}_{1}}\left( {{n}_{1}}-1 \right)}{2}\Rightarrow {{n}_{1}}=3$
*Chiếu $\large f_1$ đối  với đám nguyên tử thứ nhất thì số quỹ đạo tương ứng:
 $\large 10=\dfrac{{{n}_{2}}\left( {{n}_{2}}-1 \right)}{2}\Rightarrow {{n}_{2}}=5$
Năng lượng:  $\large \varepsilon =hf={{E}_{cao}}-{{E}_{thap}}$
 $\large \dfrac{{{f}_{1}}}{{{f}_{2}}}=\dfrac{-\dfrac{{{E}_{0}}}{n_{1}^{2}}-\left( -\dfrac{{{E}_{0}}}{{{l}^{2}}} \right)}{-\dfrac{{{E}_{0}}}{n_{2}^{2}}-\left( -\dfrac{{{E}_{0}}}{{{l}^{2}}} \right)}=\dfrac{-\dfrac{1}{{{3}^{3}}}+\dfrac{1}{{{l}^{2}}}}{-\dfrac{1}{{{5}^{2}}}+\dfrac{1}{{{1}^{2}}}}=\dfrac{25}{27}$