Hai chất điểm A và B dao động trên hai trục của hệ trục tọa độ Oxy (O

Hai chất điểm A và B dao động trên hai trục của hệ trục tọa độ Oxy (O là vị trí cân bằng của 2 vật) với phương trình lần lượt là: $\large x_A = 4\cos\left(10\pi t + \dfrac{\pi}{6}\right) cm$ và $\large x_B = 4\cos\left(10\pi t + \dfrac{\pi}{3}\right)cm$. Khoảng cách lớn nhất giữa A và B là

• A. A. 5,86 cm
• B. B. 5,26 cm
• C. C. 5,46 cm
• D. D. 5,66 cm

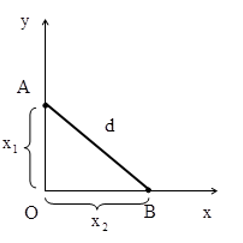
Khoảng cách giữa hai chất điểm

$\large d = \sqrt{x_A^{2} + x_B^{2}} = 4\sqrt{\underset{y}{\underbrace{\cos^{2}\left(10\pi t + \dfrac{\pi}{6}\right) + \cos^{2}\left(10\pi t + \dfrac{\pi}{3}\right)}}}$

Để d là lớn nhất thì y phải lớn nhất, biến đổi toán học ta thu được:

$\large y = 1 + \dfrac{1}{2}\cos\left(20\pi t + \dfrac{\pi}{3}\right) + \dfrac{1}{2}\cos\left(20\pi t + \dfrac{2\pi}{3}\right)$

Sử dungh công thức cộng lượng giác

$\large y = 1 + \dfrac{\sqrt{3}}{2}\sin(20\pi t) \Rightarrow y_{max} = 1 + \dfrac{\sqrt{3}}{2}$

Vậy $\large d_{max} = 4\sqrt{y_{max}} = 4\sqrt{1+ \dfrac{\sqrt{3}}{2}} \approx 5,46 cm$