Đặt điện áp xoay chiều u=U0cos(100πt+φ) vào hai đ

MỤC LỤC
Câu hỏi:
Đặt điện áp xoay chiều u=U0cos(100πt+φ) vào hai đầu đoạn mạch mắc nối tiếp gồm R1,R2 và cuộn dây thuần cảm có độ tự cảm L thay đổi được. Biết R1=2R2=50√3Ω. Điều chỉnh giá trị của L cho đến khi điện áp tức thời giữa hai đầu đoạn mạch chứa R2 và L lệch pha cực đại so với điện áp tức thời hai đầu mạch. Giá trị của L khi đó là?
Đáp án án đúng là: C
Lời giải chi tiết:
Phương pháp:
Vẽ giản đồ vecto và áp dụng công thức tan của một tổng, từ đó rút ra tana và xét giá trị cực đại.
Lời giải:
Ta có giản đồ vecto:
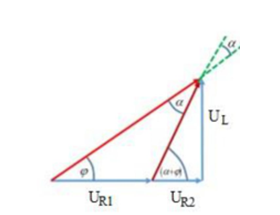
tan(φ+α)=ZLR2⇔tanφ+tanα1−tanφtanα=ZLR2⇒R2.tanφ+R2.tanα=ZL−ZL.tanφtanα
⇔(Z2LR1+R2+R2).tanα=ZL−R2.ZLR1+R2⇔R2.ZLR1+R2+R2.tanφ=ZL−ZL.ZLR1+R2.tanα
⇔[Z2L+(R1+R2).R2].tanα=ZL.R1⇒tanα=ZL.R1Z2L+(R1+R2).R2=R1ZL+(R1+R2).R2ZL
⇒αmax⇔ZL=√(R1+R2).R2=75Ω⇒L=34πH
Chọn C.
Xem thêm các bài tiếp theo bên dưới
- Trong môi trường đẳng hướng và không hấp thụ âm có ba điểm thẳng hàng
- Một vật dao động điều hòa theo phương trình $\large x=A\cos (\omega t+
- Trong dao động cưỡng bức, phát biểu nào sau đây là đúng? A. Dao động c
- Một con lắc lò xo gồm lò xo có độ cứng k và vật nhỏ có khối lượng m. C
- Trong các kí hiệu sau, kí hiệu nào là của electron? A. 10e