Con lắc lò xo gồm một lò xo có độ cứng 80 N/m và vật nặng có khối lượn

Con lắc lò xo gồm một lò xo có độ cứng 80 N/m và vật nặng có khối lượng 200 g dao động điều hoà theo phương thẳng đứng với biên độ 5 cm. Lấy $\Large g=10m/s^{2}$. Trong một chu kỳ T, khoảng thời gian lò xo bị nén là 

• A.

  $\Large \dfrac{\pi}{30}s$

• B.

  $\Large \dfrac{\pi}{60}s$

• C.

  $\Large \dfrac{\pi}{24}s$

• D.

  $\Large \dfrac{\pi}{15}s$

Phương pháp: 
Tần số góc của con lắc lò xo: $\Large \omega=\sqrt{\dfrac{k}{m}}$
Độ giãn của lò xo khi ở VTCB: $\Large \Delta l=\dfrac{mg}{k}$
Sử dụng vòng tròn lượng giác và công thức: $\Large \Delta t=\dfrac{\Delta \varphi}{\omega}$
Cách giải: 
Tần số của con lắc là: $\Large \omega=\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{80}{0,2}}=20(rad/s)$
Khi vật ở VTCB, lò xo giãn một đoạn: 
 $\Large \Delta l=\dfrac{mg}{k}=\dfrac{0,2.10}{80}=0,025(m)=2,5(cm)=\dfrac{A}{2}$
Ta có vòng tròn lượng giác: 
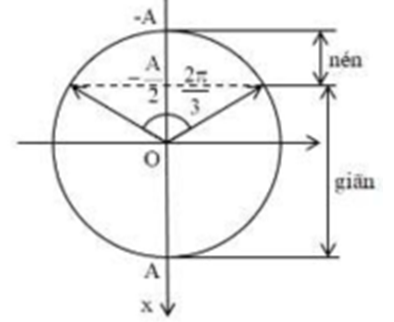 Từ vòng tròn lượng giác, ta thấy trong khoảng thời gian lò xo nén trong 1 chu kì, vecto quay được góc: 

$\Large \Delta \varphi=\dfrac{2\pi}{3}(rad)\rightarrow \Delta t_{nen}=\dfrac{\Delta \varphi}{\omega}=\dfrac{\dfrac{2\pi}{3}}{20}=\dfrac{\pi}{30}(s)$