Có một cốc thủy tinh hình trụ, bán kính trong lòng đấy cốc là 6 cm, ch
MỤC LỤC
Câu hỏi:
Có một cốc thủy tinh hình trụ, bán kính trong lòng đấy cốc là 6 cm, chiều cao trong lòng cốc là 10 cm đang đựng một lượng nước. Tính thể tích lượng nước trong cốc, biết khi nghiêng các nước vừa lúc khi nước chạm miệng cốc thì ở đáy mực nước trùng với đường kính đáy.

Đáp án án đúng là: A
Lời giải chi tiết:
Đặt R=6(cm), h = 10(cm). Gán hệ trục tọa độ như hình vẽ.
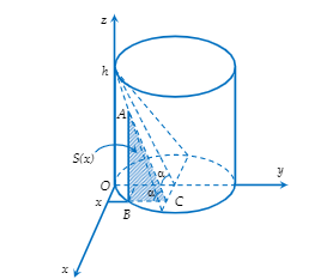
Một mặt phẳng tùy ý vuông góc với trục Ox tại điểm x (-6$\Large\le x \le$ 6) cắt vật thể theo thiết diện có diện tích là S(x).
Ta thấy thiết diện đó là một tam giác vuông, giả sử là tam giác ABC vuông tại B như trong hình vẽ.
Ta có $\Large\mathrm{S(x)=S_{A S C}=\dfrac{1}{2} A B . B C=\dfrac{1}{2} B C^{2} \tan \alpha=\dfrac{1}{2}\left(R^{2}-x^{2}\right) \dfrac{h}{R}=\dfrac{5\left(36-x^{2}\right)}{6}}$
Vậy thể tích lượng nước trong cốc là $\Large\mathrm{V=\int\limits_{-6}^{6} S(x) \mathrm{d} x=\int\limits_{-6}^{6} \dfrac{5\left(36-x^{2}\right)}{6} \mathrm{d} x=240\left(\mathrm{cm}^{3}\right)}$
Xem thêm các bài tiếp theo bên dưới
- Biết hàm số $\Large\mathrm{f(x)=(6 x+1)^2}$ có một nguyên hàm là $\Lar
- Nguyên hàm của hàm số $\Large\mathrm{y=\sqrt{\dfrac{x+1}{x-2}} . \dfra
- Cho hàm số $\Large\mathrm{f}(\mathrm{x})$ xác định trên $\Large\mathbb
- Một chất điểm G xuất phát từ 0, chuyển động thẳng với vận tốc biến thi
- Cho nguyên hàm $\Large\mathrm{I=\int \dfrac{\sqrt{x+2}}{x+6+4 \sqrt{x+