Có hai tụ điện $C_1$ và $C_2$ và hai cuộn cảm thuần $L_1$,$L_2$, Biết

Có hai tụ điện $C_1$ và $C_2$ và hai cuộn cảm thuần $L_1$,$L_2$, Biết $C_1$=$C_2$=0,2$\mu H$. Ban đầu tích điện cho tụ $C_1$ đến hiệu điện thế 8V và tụ $C_2$ đến hiệu điện thế 16V rồi cùng một lúc mắc $C_1$ với $L_1$, $C_2$ với $L_2$ để tạo thành mạch dao động lí tưởng ${{L}_{1}}{{C}_{1}}$ và${{L}_{2}}{{C}_{2}}$. Lấy ${{\pi }^{2}}=10$ thời gian ngắn nhất kể từ khi hai mạch bắt đầu dao động đến khi hiệu điện thế trên hai tụ ${{C}_{1}}$ và${{C}_{2}}$ chênh lệch nhau 4V là

• A. $\frac{{{10}^{-6}}}{3}s$
• B. $\frac{{{2.10}^{-6}}}{3}s$
• C. $\frac{{{10}^{-6}}}{6}s$
• D. $\frac{{{10}^{-6}}}{12}s$

Phương pháp: sử dụng đường tròn lượng giác

Cách giải: tần số của mạch 1 và mạch 2:

${{\omega }_{1}}={{\omega }_{2}}=\frac{1}{\sqrt{{{L}_{1}}{{C}_{1}}}}=\frac{1}{\sqrt{{{2.10}^{-6}}.0,{{2.10}^{-6}}}}=5\pi {{.10}^{5}}(rad/s)$

Phương trình hiệu điện thế của mạch 1 và 2

${{u}_{1}}=8\cos \left( 5\pi {{10}^{5}}t \right)$(1)

${{u}_{2}}=16\cos \left( 5\pi {{10}^{5}}t \right)$(2)

Từ (1) và (2) suy ra $\Delta u={{u}_{2}}-{{u}_{1}}=8\cos \left( 5\pi {{.10}^{5}}t \right)$

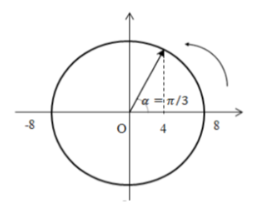
Biểu diễn trên đường tròn lượng giác ta có:

Góc quét được: $\alpha =\frac{\pi }{3}\Rightarrow \Delta t=\frac{\alpha }{\omega }=\frac{\pi }{3,5\pi {{.10}^{5}}}=\frac{{{2.10}^{-6}}}{3}s$