Cho phương trình $\Large m\mathrm{ln}(x+1)-x-2=0.$ Biết rằng tập hợp t

Cho phương trình $\Large m\mathrm{ln}(x+1)-x-2=0.$ Biết rằng tập hợp tất cả các giá trị của tham số m để phương trình đã cho có hai nghiệm $\Large x_1, x_2$ thỏa mãn $\Large 0 < x_1 < 2 < 4 < x_2$ là khoảng $\Large (a; +\infty).$ Khi đó a thuộc khoảng nào dưới đây?

• A.

  $\Large (3,7; 3,8).$

• B.

  $\Large (3,6; 3,7).$

• C.

  $\Large (3,8; 3,9).$

• D.

  $\Large (3,5; 3,6).$

Chọn A

Xét trên khoảng $\Large (0; +\infty)$ phương trình: $\Large m\mathrm{ln}(x+1)-x-2=0 \Leftrightarrow m=\dfrac{x+2}{\mathrm{ln}(x+1)}$

Đặt $\Large f(x)=\dfrac{x+2}{\mathrm{ln}(x+1)}, x \in (-1; +\infty) \setminus \begin{Bmatrix} 0 \end{Bmatrix}$

Với yêu cầu của đề bài ta xét $\Large f(x)$ trên 2 khoảng $\Large (0; 2)$ và $\Large (4; +\infty)$

$\Large {f}'(x)=\dfrac{\mathrm{ln}(x+1)-(x+2)\dfrac{1}{x+1}}{\mathrm{ln}^2(x+1)}$

Đặt $\Large g(x)=\mathrm{ln}(x+1)-(x+2)\dfrac{1}{x+1}, x\in (0; 2) \cup (4; +\infty)$

$\Large {g}'(x)=\dfrac{1}{x+1}+\dfrac{1}{(x+1)^2} > 0, \forall x \in (0; 2) \cup (4; +\infty)$

Suy ra $\Large \left\{\begin{align} & g(x) < g(2)=\mathrm{ln}3-\dfrac{4}{3} < 0, \forall x \in (0; 2) \Rightarrow {f}'(x) < 0, \forall x \in (0; 2) \\ & g(x) > g(5)=\mathrm{ln}5-\dfrac{6}{5} > 0, \forall x \in (4; +\infty) \Rightarrow {f}'(x) > 0, \forall x \in (4; +\infty) \end{align}\right.$

Từ đó ta có bảng biến thiên

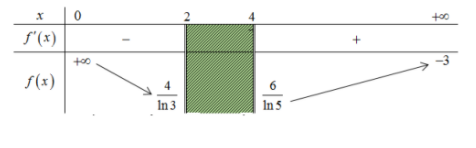
Dựa vào bảng biến thiên, để phương trình đề bài có 2 nghiệm phân biệt thỏa $\Large 0 < x_1 < 2 < 4 < x_2 \Leftrightarrow m > \dfrac{6}{\mathrm{ln}5} (\approx 3,728)$