Cho mặt cầu ( S ) có bán kính bằng 4, hình trụ ( H ) có chiều cao bằng

Cho mặt cầu (S) có bán kính bằng 4, hình trụ (H) có chiều cao bằng 4 và hai đường tròn đáy nằm trên (S). Gọi $\large V_{1}$ là thể tích của khối trụ (H) và $\large V_{2}$ là thể tích của khối cầu (S). Tính tỉ số $\large \dfrac{V_{1}}{V_{2}}$.

• A.

  A. $\large \dfrac{V_{1}}{V_{2}} = \dfrac{9}{16}$

• B.

  B. $\large \dfrac{V_{1}}{V_{2}} = \dfrac{1}{3}$

• C.

  C. $\large \dfrac{V_{1}}{V_{2}} = \dfrac{3}{16}$

• D.

  D. $\large \dfrac{V_{1}}{V_{2}} = \dfrac{2}{3}$

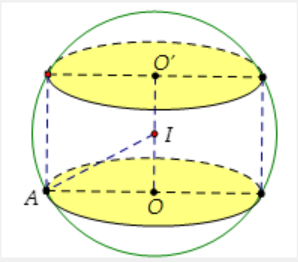
Theo đề ra ta có

$\large \left\{\begin{matrix} R_{c} = IA = 4 & \\  h = OO' = 4 \Rightarrow OI = 2 &  \end{matrix}\right.$ 

Suy ra: $\large R_{tru} = OA = \sqrt{IA^{2}-IO^{2}} = \sqrt{4^{2}-2^{2}} = 2\sqrt{3}$ 

$\large \Rightarrow \left\{\begin{matrix} V_{1} = h\pi R_{tru}^{2} = 4\pi .(2\sqrt{3})^{2} = 48\pi & \\  V_{2} = \dfrac{4}{3}\pi R_{c}^{3} = \dfrac{4}{3}\pi .4^{3} = \dfrac{256\pi }{3} &  \end{matrix}\right.\Rightarrow \dfrac{V_{1}}{V_{2}} = \dfrac{48\pi }{\dfrac{256\pi }{3}} = \dfrac{9}{16}$