Cho mặt cầu $\large (S): x^2+y^2+z^2-2x-2y-2z=0$. Điểm A(2;2;0). Viết

Cho mặt cầu $\large (S): x^2+y^2+z^2-2x-2y-2z=0$. Điểm A(2;2;0). Viết phương trình mặt phẳng (OAB) biết điểm B là một điểm thuộc mặt cầu (S), có hoành độ dương và tam giác OAB đều.

 

• A. A. x - y + 2z = 0
• B. B. x - y - 2z = 0
• C. C. x - y - z = 0
• D. D. 2 - y + z = 0

Gọi B (x; y; z), với x > 0 và H trung điểm OA $\largư \Rightarrow $ H(1; 1; 0)

Gọi (P) là mặt phẳng trung trực đoạn OA, Ta có (P) đi qua trung điểm H (1; 1; 0) của đoạn OA và nhận $\large \vec{OA}=(2; 2; 0)$ là một vecto pháp tuyến 

Suy ra phương trình (P) là $\large 2(x-1)+2(y-1)=0\Leftrightarrow x+y-2=0$

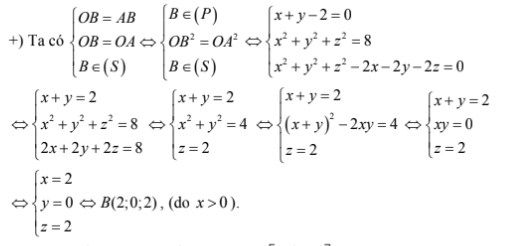
Ta có: $\large \overrightarrow{OA}=(2;2;0); \overrightarrow{OB}=(2;0;2)\Rightarrow \left[\overrightarrow{OA},\overrightarrow{OB}\right]=(-4;-4;-4)=4(-1;-1;-1)$

Mặt phẳng (OAB) đi qua, nhận  $\large \vec{n}=(1;-1;-1)$ là một vecto pháp tuyến

Vậy phương trình (OAB) là $\large x-y-z=0$