Cho mạch điện như hình vẽ. Điện áp xoay chiều ổn định giữa hai đầu A v

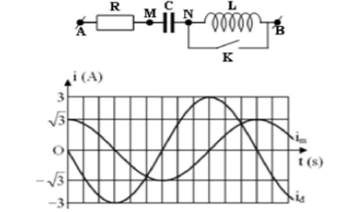
Cho mạch điện như hình vẽ. Điện áp xoay chiều ổn định giữa hai đầu A và B là $\Large u=120\sqrt{3}cos(\omega t+\varphi) (V).$ Khi K mở hoặc đóng thì cường độ dòng điện qua mạch theo thời gian tương ứng là im và id  được biểu diễn như hình bên. Giá trị của R bằng

• A.

  $\Large 60\Omega .$

• B.

  $\Large 60\sqrt{2}\Omega.$

• C.

  $\Large 30\sqrt{3}\Omega.$

• D.

  $\Large 30\Omega.$

Phương pháp:
+ Đọc đồ thị i-t
+ Sử dụng biểu thức định luật ôm: $\Large I=\dfrac{U}{Z}$
+ Sử dụng biểu thức tính hệ số công suất: $\Large cos\varphi=\dfrac{R}{Z}$
Cách giải:
Ta có:
+ Khi K mở, mạch gồm R, L, C mắc nối tiếp 
Từ đồ thị ta thấy: $\Large i_m=\sqrt{3}cos\left(\omega t+\dfrac{\pi}{2}\right)$
Tổng trở của mạch: $\Large Z_m=\dfrac{U_0}{I_0}=\dfrac{120\sqrt{3}}{\sqrt{3}}=120\Omega$ và $\Large Z_m=\sqrt{R^2+(Z_L-Z_C)^2} \ (1)$  
+ Khi K đóng, mạch gồm R nối tiếp với C
Từ đồ thị ta thấy: $\Large i_d=3cos(\omega t)$
Tổng trở của mạch: $\Large Z_d=\dfrac{U_0}{I_0}=\dfrac{120\sqrt{3}}{3}=40\sqrt{3}\Omega$ và $\Large Z_d=\sqrt{R^2+Z_C^2} \ (2)$  
Ta thấy: $\Large i_m \perp i_d \Rightarrow \varphi_m +\varphi_d=\dfrac{\pi}{2} \Rightarrow cos^2\varphi_m+cos^2\varphi_d=1$
Ta có: $\Large \left\{\begin{align} & cos\varphi_m=\dfrac{R}{Z_m}=\dfrac{R}{\sqrt{R^2+(Z_L-Z_C)^2}} \\ & cos\varphi_d=\dfrac{R}{Z_d}=\dfrac{R}{\sqrt{R^2+Z_C^2}} \end{align}\right.$
Ta suy ra: $\Large \dfrac{R^2}{120^2}+\dfrac{R^2}{(40\sqrt{3})^2}=1 \Rightarrow R=60 \Omega$
Chọn A.