Cho $\Large (H)$ là hình phẳng giới hạn bởi parabol $\Large y=\dfrac{{
Lưu về Facebook:
MỤC LỤC
Câu hỏi:
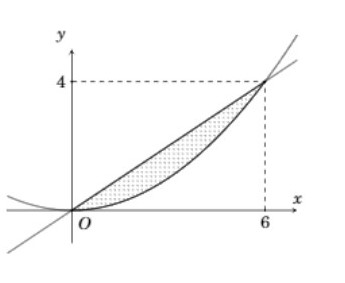
Cho $\Large (H)$ là hình phẳng giới hạn bởi parabol $\Large y=\dfrac{{{x}^{2}}}{9}$ và đường thẳng $\Large -2x+3y=0$. Tính thể tích $\Large V$ của khối tròn xoay khi quay hình phẳng $\Large (H)$ (phần tô sọc) quanh trục hoành.

Đáp án án đúng là: C
Lời giải chi tiết:
Dựa vào hình vẽ ta có $\Large V=\pi \int\limits_{0}^{6}{\left[ {{\left( \dfrac{2x}{3} \right)}^{2}}-{{\left( \dfrac{{{x}^{2}}}{9} \right)}^{2}} \right]dx}$ $\Large =\pi \int\limits_{0}^{6}{\left( \dfrac{4{{x}^{2}}}{9}-\dfrac{{{x}^{4}}}{81} \right)dx}$ $\Large = \left( \dfrac{4{{x}^{3}}}{27}-\dfrac{{{x}^{5}}}{405} \right)\left| \begin{align} & 6 \\ & 0 \\ \end{align} \right.$ $\Large = \dfrac{64\pi }{5}$
Chọn đáp án C
Xem thêm các bài tiếp theo bên dưới
- Biết $\Large I=\int\limits_{2}^{5}{\dfrac{\left| x-2 \right|}{x}dx=a\l
- Cho hàm số $\Large f(x)$ liên tục trên [-1;4] và có đồ thị trên [-1;4]
- Có bao nhiêu giá trị thực của $\Large a$ để có $\Large \int\limits_{0}
- Cho hàm số $\Large f(x)=\left\{ \begin{align} & x,khi,x\ge 1 \\ & 1,kh
- Bổ dọc một quả dưa hấu ta được thiết diện là hình elip có trục lớn 28