Cho khối tứ diện <span class="MathJax_Preview" style="color: inherit; display: none;"></span><span id="MathJax-Element-1-Frame" class="mjx-chtml MathJax_CHTML" tabindex="0" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mstyle mathsize="1.2em"><mi>A</mi><mi>B</mi><mi>C</mi><mi>D</mi></mstyle></math>" role="presentation" style="font-size: 127%; position: relative;"><span id="MJXc-Node-1" class="mjx-math" aria-hidden="true"><span id="MJXc-Node-2" class="mjx-mrow"><span id="MJXc-Node-3" class="mjx-mstyle"><span id="MJXc-Node-4" class="mjx-mrow" style="font-size: 120%;"><span id="MJXc-Node-5" class="mjx-mi"><span class="mjx-char MJXc-TeX-math-I" style="padding-top: 0.495em; padding-bottom: 0.298em;">A</span></span><span id="MJXc-Node-6" class="mjx-mi"><span class="mjx-char MJXc-TeX-math-I" style="padding-top: 0.445em; padding-bottom: 0.298em;">B</span></span><span id="MJXc-Node-7" class="mjx-mi"><span class="mjx-char MJXc-TeX-math-I" style="padding-top: 0.495em; padding-bottom: 0.298em; padding-right: 0.045em;">C</span></span><span id="MJXc-Node-8" class="mjx-mi"><span class="mjx-char MJXc-TeX-math-I" style="padding-top: 0.445em; padding-bottom: 0.298em;">D</span></span></span></span></span></span><span class="MJX_Assistive_MathML" role="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mstyle mathsize="1.2em"><mi>A</mi><mi>B</mi><mi>C</mi><mi>D</mi></mstyle></math></span></span><script type="math/tex" id="MathJax-Element-1">\large ABCD</script>. Lấy một điểm <span class="MathJax_Preview" style="color: inherit; display: none;"></span><span id="MathJax-Element-2-Frame" class="mjx-chtml MathJax_CHTML" tabindex="0" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mstyle mathsize="1.2em"><mi>M</mi></mstyle></math>" role="presentation" style="font-size: 127%; position: relative;"><span id="MJXc-Node-9" class="mjx-math" aria-hidden="true"><span id="MJXc-Node-10" class="mjx-mrow"><span id="MJXc-Node-11" class="mjx-mstyle"><span id="MJXc-Node-12" class="mjx-mrow" style="font-size: 120%;"><span id="MJXc-Node-13" class="mjx-mi"><span class="mjx-char MJXc-TeX-math-I" style="padding-top: 0.445em; padding-bottom: 0.298em; padding-right: 0.081em;">M</span></span></span></span></span></span><span class="MJX_Assistive_MathML" role="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><mstyle mathsize="1.2em"><mi>M</mi></mstyle></math></span></span><script type="math/tex" id="MathJax-Element-2">\large M</script> nằm giữa $\lar

Cho khối tứ diện $\large ABCD$ . Lấy một điểm $\large M$ nằm giữa $\lar

4/5

Tác giả: Thầy Tùng

Đăng ngày: 18 Aug 2022

Lưu về Facebook:

$Hình minh họa Cho khối tứ diện $\large ABCD$. Lấy một điểm $\large M$ nằm giữa $\lar$

MỤC LỤC

Lời giải chi tiết

Câu hỏi:

Cho khối tứ diện $\large ABCD$ . Lấy một điểm $\large M$ nằm giữa $\large A$ và $\large B$ , một điểm $\large N$ nằm giữa $\large C$ và $\large D$ . Bằng hai mặt phẳng $\large (MCD)$ và $\large (NAB)$ ta chia khối tứ diện đã cho thành bốn khối tứ diện:

A.
A. AMCD, AMND, BMCN, BMND
B.
B. AMCN, AMND, BMCN, BMND
C.
C. AMCN, BMNC, AMDN, BMND
D.
D. AMCN, AMND, AMCD, BMCD

Đáp án án đúng là: C

Lời giải chi tiết:

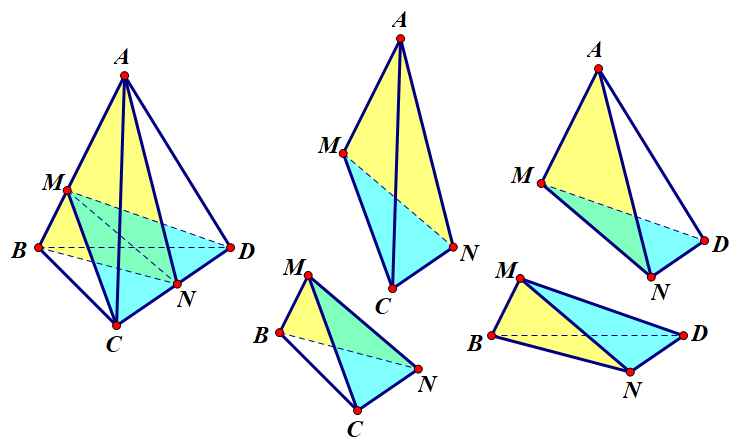
$Hình đáp án 1. Cho khối tứ diện $\large ABCD$. Lấy một điểm $\large M$ nằm giữa $\lar$
Ban đầu, mặt $\large (NAB)$ chia khối tứ diện $\large ABCD$ thành 2 khối đa diện: $\large ABCN,ABDN$ . Tiếp đến, mặt $\large (MCD)$ chia:

+) $\large ABCN$ thành $\large AMCN$ và $\large BMNC$

+) $\large ABDN$ thành $\large AMDN$ và $\large BMND$

Vậy hai mặt phẳng $\large (MCD)$ và $\large (NAB)$ ta chia khối tứ diện đã cho thành bốn khối tứ diện.

$\large AMCN,BMNC,AMDN,BMND$

Đáp án C

Xem thêm các bài tiếp theo bên dưới