Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2 a , khoảng cách từ
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a, khoảng cách từ tâm O của đường tròn ngoại tiếp của đáy ABC đến một mặt bên là . Thể tích của khối nón ngoại tiếp hình chóp S.ABC bằng:
Đáp án án đúng là: B
Lời giải chi tiết:
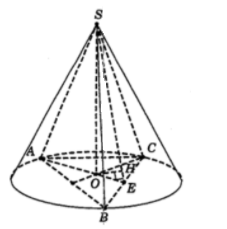
Gọi E là trung điểm của BC, dựng tại H.
Chứng minh được nên suy ra OH = d[O,(SBC)] =
Trong tam giác đều ABC, ta có
Trong tam giác vuông SOE, ta có
.
Vậy thể tích khối nón
(đvtt)
Chọn B.
Xem thêm các bài tiếp theo bên dưới
- Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và góc giữa một cạ
- Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng
- Khối nón ( N ) có chiều cao bằng 3 a . Thiết diện song song và cách mặ
- Cho hình nón ( N ) có bán kính đáy bằng 10, mặt phẳng vuông góc với tr
- Hình trụ ( T ) được sinh ra khi quay hình chữ nhật ABCD quanh cạnh AB