Cho hình chóp S.ABCD có đáy là hình vuông tâm O cạnh bằng a . Hình chi

Cho hình chóp S.ABCD có đáy là hình vuông tâm O cạnh bằng a . Hình chiếu vuông góc của đỉnh S lên mặt đáy (ABCD) là trung điểm của đoạn thẳng AO. Mặt phẳng (SBC) tạo với mặt đáy một góc $\large 45^\circ$. Tính khoảng cách giữa SD và AC

• A.

  A. $\large \dfrac{a\sqrt{38}}{17}$

• B.

  B. $\large \dfrac{a\sqrt{51}}{13}$

• C.

  C. $\large \dfrac{a\sqrt{13}}{3}$

• D.

  D. $\large \dfrac{3a\sqrt{34}}{34}$

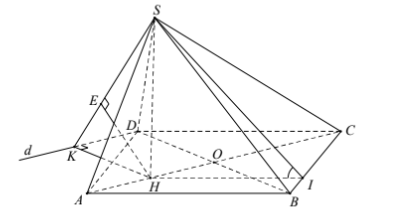
Gọi H là trung điểm của AO $\large \Rightarrow SH\perp (ABCD)$

Dựng HI vuông góc với BC tại I. Ta có góc giữa (SBC) và (ABCD) là góc $\large \widehat{SIH}$

Từ giả thiết $\large \Rightarrow \widehat{SIH}=45^\circ$

Trong mặt phẳng (ABCD) , dựng đường thẳng d đi qua điểm D và song song với đường thẳng AC

Gọi $\large (\alpha)$ là mặt phẳng chứa d và $\large SD\Rightarrow (\alpha)//AC\Rightarrow d(AC, SD)=d(AC, (\alpha))=d(H, (\alpha))$

Dựng HK vuông góc với d tại K , dựng HE vuông góc với SK tại E .
Ta có $\large \left[\begin{align}& d\perp HK\\& d\perp SH\\\end{align}\right.$ $\large \Rightarrow d\perp (SHK)\Rightarrow d\perp HE$. Lại có $\large HE\perp SK\Rightarrow HE\perp (\alpha)\Rightarrow d(H, (\alpha))=HE$

Trong tam giác ABC ta có: $\large \dfrac{HI}{AB}=\dfrac{CH}{CA}=\dfrac{3}{4}\Rightarrow HI=\dfrac{3}{4}AB=\dfrac{3a}{4}$

Trong tam giác SHI ta có $\large SH=HI.\tan45^\circ=HI=\dfrac{3a}{4}$

Tứ giác ABCD là hình vuông nên: $\large AC\perp BD\Leftrightarrow HK//BD\Rightarrow HK=OD=\dfrac{a\sqrt{2}}{2}$

Trong tam giác SHK ta có : $\large HE=\dfrac{SH.HK}{\sqrt{SH^2+HK^2}}=\dfrac{\dfrac{3a}{4}.\dfrac{a\sqrt{2}}{2}}{\sqrt{\dfrac{9a^2}{16}+\dfrac{2a^2}{4}}}=\dfrac{3a\sqrt{34}}{34}$

Vậy: $\large d(AC, SD)=\dfrac{3a\sqrt{34}}{34}$