Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và $\large SA\p
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và SA⊥(ABC). Điểm nào sau đây là tâm của mặt cầu đi qua các điểm S, A, B, C?
Đáp án án đúng là: B
Lời giải chi tiết:
Chọn B
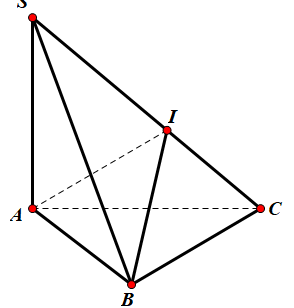
Ta có: {BC⊥SABC⊥AB ⇒BC⊥(SAB)⇒BC⊥SB
Gọi I là trung điểm của đoạn SC
Xét tam giác SAC vuông tại A, I là trung điểm của SC ⇒IS=IC=IA (1)
Xét tam giác SBC vuông tại B, I là trung điểm của SC ⇒IB=IS=IC (2)
Từ (1) và (2) ⇒IA=IB=IS=IC⇒ I là tâm mặt cầu đi qua bốn điểm S, A, B, C
Xem thêm các bài tiếp theo bên dưới
- Trong không gian Oxyz, mặt phẳng (P) đi qua A(0; 0; -1) và nhận $\larg
- Qua phép chiếu song song, tính chất nào không được bảo toàn? Song song
- Cho số phức z=−2+3i. Trên mặt phẳng tọa đọ Oxy, điểm biểu di
- Cho tam giác vuông ABC có $\large \widehat{BAC} = 90^\circ;\, AB = a;\
- Trong không gian Oxyz, cho $\large \vec{a} =-\vec{i} + 2\vec{j} - 3\ve