Cho hình chóp $\Large S.ABC$ có đáy $\Large ABC$ là tam giác vuông cân

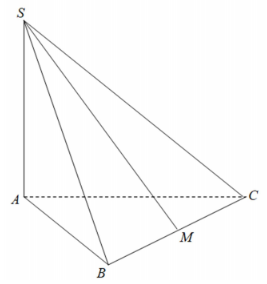
Cho hình chóp $\Large S.ABC$ có đáy $\Large ABC$ là tam giác vuông cân tại $\Large A,$ $\Large SA$ vuông góc với mặt phẳng đáy, $\Large SA=\dfrac{\sqrt{2}a}{2}, AB=AC=a.$ Gọi $\Large M$ là trung điểm của $\Large BC$ (xem hình vẽ). Tính góc giữa đường thẳng $\Large SM$ và mặt phẳng $\Large (ABC).$

• A.

  A. $\Large 90^{\circ}.$

• B.

  B. $\Large 60^{\circ}.$

• C.

  C. $\Large 30^{\circ}.$

• D.

  D. $\Large 45^{\circ}.$

Chọn D

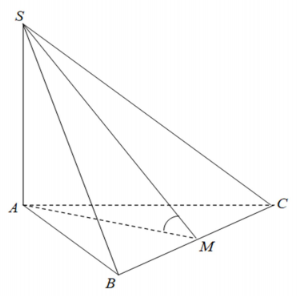
Do $\Large SA$ vuông góc với mặt phẳng $\Large (ABC)$ nên $\Large AM$ là hình chiếu vuông góc của $\Large SM$ trên mặt phẳng $\Large (ABC),$ nên góc giữa đường thẳng $\Large SM$ và mặt phẳng $\Large (ABC)$ là góc giữa $\Large SM$ và $\Large AM$ hay $\Large \widehat{SMA}.$

Vì tam giác $\Large ABC$ là tam giác vuông cân tại $\Large A$ nên $\Large AM=\dfrac{1}{2}BC=\dfrac{a\sqrt{2}}{2}.$

Tam giác $\Large SAM$ vuông tại $\Large A$ và có $\Large SA=AM=\dfrac{a\sqrt{2}}{2}$ nên tam giác $\Large SAM$ vuông cân tại $\Large A$ do đó $\Large \widehat{SMA}=45^{\circ}.$