Cho hàm số $y=f\left( x \right)$ có bảng biến thiên: Số tiệm cận đứng

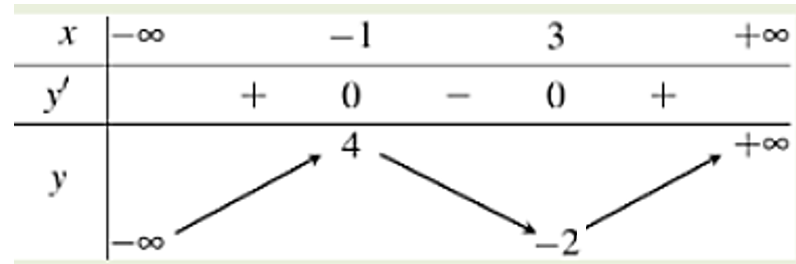
Cho hàm số $y=f\left( x \right)$ có bảng biến thiên:

Số tiệm cận đứng của đồ thị hàm số $y=\frac{2020}{f\left( x \right)}\left( f\left( x \right)\ne 0 \right)$ là:
 

• A. A. 1
• B. B. 2
• C. C. 3
• D. D. 4

Điều kiện $f\left( x \right)\ne 0$
Số tiệm cận đứng của đồ thị hàm số $y=\frac{2018}{f\left( x \right)}$ là số nghiệm của phương trình $f\left( x \right)=0$ (tức là số giao điểm của đồ thị hàm số $y=f\left( x \right)$ và trục hoành)
Nhìn bảng biến thiên ta thấy số giao điểm của đồ thị $y=f\left( x \right)$ với trục hoành bằng 3 nên đồ thị đã cho có 3 tiệm cận đứng