Cho hàm số $\Large y=f(x)$ có $\Large {f}'(x)=x(x-3)^2(x^2-2x-3)$. Số

Cho hàm số $\Large y=f(x)$ có $\Large {f}'(x)=x(x-3)^2(x^2-2x-3)$. Số điểm cực đại của hàm số $\Large f(x)$ là

• A.

  4.

• B.

  2.

• C.

  1.

• D.

  3.

Chọn C

Ta có $\Large {f}'(x)=0$ $\Large \Leftrightarrow \left[\begin{align} & x=0\\ & x-3=0\\ & x^2-2x-3=0 \end{align}\right.$ $\Large \Leftrightarrow \left[\begin{align} & x=0\\ & x=3\\ & x=-1\end{align}\right.$

Bảng biến thiên:

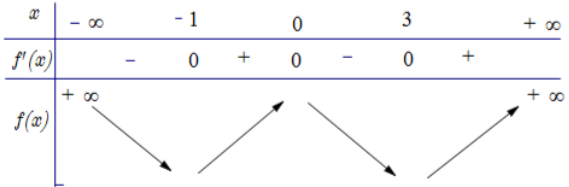
Vậy hàm số $\Large f(x)$ có một điểm cực đại.