Vị trí tương đối của mặt cầu với mặt phẳng, đường thẳng

 Vị trí tương đối giữa mặt cầu và mặt phẳng

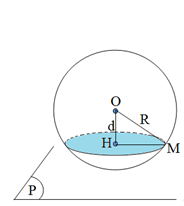
Cho mặt cầu $S(O;R)$ và mặt phẳng $(P)$. Gọi $H$ là hình chiếu của $O$ trên mặt phẳng $(P)$ và đặt $d = d(O;(P)) = OH$. Khi đó:

• Nếu $d < R$ thì thì mp$(P)$ cắt mặt cầu $S(O:R)$ theo giao tuyến là đường tròn nằm trên mp$(P)$  có tâm là $H$ và bán kính $r = \sqrt{R^2 - d^2}$.

Khi $d = 0$ thì mp$(P)$ đi qua tâm $O$ của mặt cầu, mặt phẳng đó được gọi là mặt phẳng kính, giao tuyến của mặt phẳng kính với mặt cầu là đường tròn có bán kính $R$ gọi là đường tròn lớn của mặt cầu

• Nếu $d = R$ thì mp$(P)$ cắt mặt cầu tại một điểm duy nhất $H$.

Khi đó ta nói mặt phẳng $(P)$ tiếp xúc với mặt cầu $S(O;R)$ tại điểm $H$ hoặc còn nói mp$(P)$ là tiếp diện của mặt cầu tại điểm $H$, điểm $H$ gọi là điểm tiếp xúc ( hoặc tiếp điểm ) của $(P)$ và mặt cầu.

• Nếu $d > R$ thì mp$(P)$ không cắt mặt cầu $S(O;R)$

 Vị trí tương đối giữa mặt cầu và đường thẳng

Cho mặt cầu $S(O;R)$ và đường thẳng  $\Delta$. Gọi $H$ là hình chiếu của $O$ trên $\Delta$ và $d = OH$ là khoảng cách từ $O$ tới  $\Delta$. Ta có:
-    Nếu $d < R$ thì $\Delta$ cắt mặt cầu tại 2 điểm phần biệt
  
-    Nếu $d = R$ thì  $\Delta$ cắt mặt cầu tại 1 điểm duy nhất
  
-    Nếu $d > R$ thì $\Delta$ không cắt mặt cầu
  

Trong trường hợp $d = R$ người ta nói đường thẳng  $\text{ }\!\!\Delta\!\!\text{ }$ và mặt cầu $S(O;R)$ có điểm chung duy nhất là $H$. Khi đó đường thẳng  $\text{ }\!\!\Delta\!\!\text{ }$ tiếp xúc với mặt cầu tại điểm $H$ hay còn gọi  $\Delta$ là tiếp tuyến của mặt cầu, điểm $H$ gọi là tiếp điểm của  $\text{ }\!\!\Delta\!\!\text{ }$ và mặt cầu.

Định lý: Nếu 1 điểm $A$ nằm ngoài mặt cầu $S(O;R)$ thì:
a)    Qua $A$ có vô số tiếp tuyến với mặt cầu
b)    Độ dài các đoạn thẳng nối $A$ với các tiếp điểm bằng nhau
c)    Tập hợp các tiếp điểm là 1 đường tròn nằm trên mặt cầu