Đối xứng tâm
Lý thuyết về Đối xứng tâm
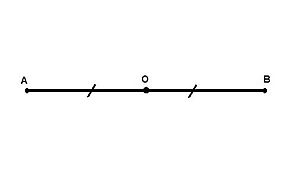
Hai điểm đối xứng qua một điểm.
Định nghĩa: Hai điểm gọi là đối xứng với nhau qua điểm OO nếu OO là trung điểm của đoạn thẳng nối hai điểm đó.
Hai hình đối xứng qua một điểm.
Định nghĩa: Hai hình gọi là đối xứng với nhau qua điểm OO nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua điểm OO và ngược lại. Điểm OO gọi là tâm đối xứng của hai hình đó.
Hình có tâm đối xứng.
Định nghĩa: Điểm OO gọi là tâm đối xứng qua hình HH nếu điểm đối xứng với mỗi điểm thuộc hình HH qua điểm OO cũng thuộc hình HH.
Định lí: Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó.
Bài tập tự luyện có đáp án
Câu 1: Khẳng định sai là
- A
- B
- C
- D
Đường tròn có duy nhất một tâm đối xứng chính là tâm của đường tròn đó
Câu 2: Trong các mệnh đề sau, mệnh đề nào đúng?
- A
- B
- C
- D
Hình bình hành có tâm đối xứng chính là giao điểm hai đường chéo của nó.
Mọi tam giác đều không có tâm đối xứng.
Hình thang cân không có tâm đối xứng.
Câu 3: Chọn khẳng định sai trong các khẳng định sau
- A
- B
- C
- D
Mọi tam giác đều không có tâm đối xứng nên khẳng định Trọng tâm của một tam giác là tâm đối xứng của tam giác đó là khẳng định sai
Câu 4: Hãy chọn câu sai.
- A
- B
- C
- D
+ Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó.
+ Đường tròn là hình có tâm đối xứng là tâm của đường tròn.
+ Giao điểm hai đường chéo của hình vuông là tâm đối xứng của hình vuông đó.
+ Hình thang không có tâm đối xứng.
Câu 5: Hình nào sau đây không có tâm đối xứng?
- A
- B
- C
- D
Hình thoi (và cả hình vuông, hình chữ nhật, hình bình hành) có tâm đối xứng chính là giao điểm hai đường chéo.
Hình tròn có tâm đối xứng chính là tâm đường tròn đó.
Tam giác bất kỳ đều không có tâm đối xứng
Câu 6: Khẳng định đúng là
- A
- B
- C
- D
Định nghĩa về Hai điểm đối xứng qua một điểm
Câu 7: Trong các hình sau đây, hình nào không có tâm đối xứng?
- A
- B
- C
- D
Vì mọi tam giác đều không có tâm đối xứng.
Câu 8: Hãy chọn câu sai.
- A
- B
- C
- D
+ Theo định nghĩa hai điểm đối xứng qua một điểm: Hai điểm AA , BB gọi là đối xứng với nhau qua điểm OO nếu OO là trung điểm của đoạn thẳng nối hai điểm đó.
+ Trung điểm của đoạn thẳng là tâm đối xứng duy nhất của đoạn thẳng đó.
+ Hình bình hành có một tâm đối xứng là giao hai đường chéo.
+ Điểm đối xứng của một điểm MM qua MM chính là MM .
Xem thêm các bài tiếp theo bên dưới