Định luật Bôi- lơ Ma- ri - ôt
Lý thuyết về Định luật Bôi- lơ Ma- ri - ôt
Quá trình đẳng nhiệt là quá trình biến đổi trạng thái khi nhiệt độ không đổi
Trong quá trình đẳng nhiệt của một khối lượng khí xác định, áp suất tỉ lệ nghịch với thể tích.
p˜ 1Vp~ 1V hay pV = hằng số
Hoặc: p1V1=p2V2=…p1V1=p2V2=…
Trong đó:
p1;p2p1;p2 là áp suất của khí lí tưởng ở trạng thái 1 và trạng thái 2
V1;V2V1;V2 là thể tích của khí ở trạng thái 1 và trạng thái 2
Bài tập tự luyện có đáp án
Câu 1: Một bình có thể tích 5,6 ℓ chứa 0,5 mol khí ở 00C00C , áp suất trong bình là
- A
- B
- C
- D
1 mol khí ở đktc (0oC, p=1p=1 atm) có V=22,4ℓV=22,4ℓ → ở đktc 0,5 moℓ có V=11,2ℓV=11,2ℓ
Trạng thái 1: T1=0oC;p1=1atm;V1=11,2ℓT1=0oC;p1=1atm;V1=11,2ℓ
Trạng thái 2: T2=0oC;p2=?;V2=5,6ℓT2=0oC;p2=?;V2=5,6ℓ
T1=T2→p1V1=p2V2↔1.11,2=p2.5,6→p2=2atmT1=T2→p1V1=p2V2↔1.11,2=p2.5,6→p2=2atm .
Câu 2: Một bình kín đựng khí Heli chứa N=1,505.1023N=1,505.1023 nguyên tử khí Heli ở 0oC0oC và có áp suất trong bình là 2 atm. Thể tích của bình đựng khí là
- A
- B
- C
- D
Một mol khí chứa 6,02.10236,02.1023 phân tử → 1,505.10231,505.1023 phân tử ứng với 0,25 mol
1 mol khí ở đktc ( 0oC0oC , p=1p=1 atm) có V=22,4ℓV=22,4ℓ → ở đktc 0,25 moℓ có V=5,6ℓV=5,6ℓ
Trạng thái 1: T1=0oC;p1=1atm;V1=5,6ℓT1=0oC;p1=1atm;V1=5,6ℓ (0,25 mol khí ở đktc)
Trạng thái 2: T2=0oC;p2=2atm;V2=?ℓT2=0oC;p2=2atm;V2=?ℓ (0,25 mol khí ở trong bình)
Do T1=T2→p1V1=p2V2↔1.5,6=2.V2→V2=2,8ℓ.T1=T2→p1V1=p2V2↔1.5,6=2.V2→V2=2,8ℓ.
Câu 3: Một bình kín đựng khí Heli chứa N=1,505.1023N=1,505.1023 nguyên tử khí Heli ở 0oC0oC và có áp suất trong bình là 2 atm. Thể tích của bình đựng khí là
- A
- B
- C
- D
Một mol khí chứa 6,02.10236,02.1023 phân tử → 1,505.10231,505.1023 phân tử ứng với 0,25 mol
1 mol khí ở đktc ( 0oC0oC , p=1p=1 atm) có V=22,4ℓV=22,4ℓ → ở đktc 0,25 moℓ có V=5,6ℓV=5,6ℓ
Trạng thái 1: T1=0oC;p1=1atm;V1=5,6ℓT1=0oC;p1=1atm;V1=5,6ℓ (0,25 mol khí ở đktc)
Trạng thái 2: T2=0oC;p2=2atm;V2=?ℓT2=0oC;p2=2atm;V2=?ℓ (0,25 mol khí ở trong bình)
Do T1=T2→p1V1=p2V2↔1.5,6=2.V2→V2=2,8ℓ.T1=T2→p1V1=p2V2↔1.5,6=2.V2→V2=2,8ℓ.
Câu 4: Một khối khí thực hiện quá trình được biểu diễn trên hình vẽ. Quá trình đó là quá trình


- A
- B
- C
- D
T = hằng số → Quá trình đó là quá trình đẳng nhiệt.
Câu 5: Trong các hệ thức sau đây, hệ thức nào không phù hợp với định luật Bôi-lơ Ma-ri-ốt?
- A
- B
- C
- D
Định luật Bôi-lơ Ma-ri-ốt: pV= hằng số: V tỉ lệ nghịch với p → V∼1/p hay p∼1/V
Câu 6: Ở điều kiện tiêu chuẩn: 1 mol khí ở 0oC có áp suất 1atm và thể tích là 22,4ℓ . Hỏi một bình có dung tích 5ℓ chứa 0,5 mol khí ở nhiệt độ 0oC có áp suất là bao nhiêu:
- A
- B
- C
- D
1 mol khí ở đktc ( 0oC,p=1atm ) có V=22,4ℓ → ở đktc 0,5 moℓ có V=11,2ℓ
Trạng thái 1: T1=0oC;p1=1atm;V1=11,2ℓ (0,5 mol khí ở đktc)
Trạng thái 2: T2=0oC;p2=?atm;V2=5ℓ (0,5 mol khí ở trong bình)
Có T1=T2→p1V1=p2V2↔1.11,2=p2.5→p2=2,24atm.
Câu 7: Trong quá trình đẳng nhiệt thì ta có hệ thức nào sau đây? Cho biết khối lượng riêng của chất khí là D, áp suất của khối khí là p và thể tích của khối khí là V .
Cho biết khối lượng riêng của chất khí là D, áp suất của khối khí là p và thể tích của khối khí là V .
- A
- B
- C
- D
D=mV nên V1V2=D2D1 , vì T = hằng số, nên V1V2=p2p1 , do đó D2D1=p2p1
Trong quá trình đẳng nhiệt khối lượng riêng của chất khí tỉ lệ nghịch với thể tích và tỉ lệ thuận với áp suất.
Câu 8: Trong hệ tọa độ (V,T) đường đẳng nhiệt là
- A
- B
- C
- D
Trong hệ tọa độ (V,T) , đường đẳng nhiệt là đường thẳng vuông góc với trục T :

Câu 9: Có 7 gam khí Nitơ ở điều kiện tiêu chuẩn. Người ta nén đẳng nhiệt khối khí này tới áp suất 133 cmHg thì thể tích của khối khí bây giờ là bao nhiêu?
- A
- B
- C
- D
Số mol nitơ là nN2=mM=728=0,25 mol → V1=0,25.22,4=5,6ℓ.
Thể tích này ứng với áp suất thường p1=1atm=760mmHg
Theo định luật Bôi-lơ Ma-ri-ốt: p1V1=p2V2 → V2=p1V1p2=760.5,61330=3,2ℓ=3,2dm3.
Câu 10: Điều nào sau đây sai với quá trình đẳng nhiệt của một lượng khí xác định?
- A
- B
- C
- D
Với một lượng khí xác định, khi nhiệt độ không đổi thì p,V tỉ lệ nghịch với nhau. Đường đẳng nhiệt, trong hệ trục (p,V) đường biểu diễn là một nhánh Hypeboℓ, trong hệ trục (V,T) đường
Câu 11: Định luật Bôi lơ – Mari ốt áp dụng cho quá trình
- A
- B
- C
- D
Định luật Bôi Lơ-Mariốt áp dụng cho quá trình đẳng nhiệt.
Câu 12: Trong hệ tọa độ (p,V) , đường đẳng nhiệt là
- A
- B
- C
- D
Trong hệ tọa độ (p,V) , đường đẳng nhiệt là đường hyperbol:

Câu 13: Trong hệ tọa độ (p,T) đường đẳng nhiệt là
- A
- B
- C
- D
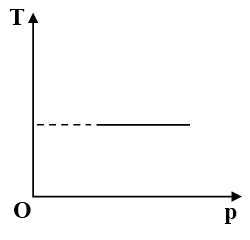
Trong hệ tọa độ (p, T) đường đẳng nhiệt là đường thẳng song song trục p :

Câu 14: Đẳng quá trình là
- A
- B
- C
- D
Đẳng quá trình là quá trình trong đó có một thông số trạng thái không đổi.
Câu 15: Trong quá trình đẳng nhiệt thì ta có hệ thức nào sau đây? Cho biết khối lượng riêng của chất khí là D, áp suất của khối khí là p và thể tích của khối khí là V .
Cho biết khối lượng riêng của chất khí là D, áp suất của khối khí là p và thể tích của khối khí là V .
- A
- B
- C
- D
D=mV nên V1V2=D2D1 , vì T = hằng số, nên V1V2=p2p1 , do đó D2D1=p2p1
Trong quá trình đẳng nhiệt khối lượng riêng của chất khí tỉ lệ nghịch với thể tích và tỉ lệ thuận với áp suất.
Câu 16: Trong các đại lượng sau đây, đại lượng nào không phải là thông số trạng thái của một lượng khí?
- A
- B
- C
- D
Trạng thái của một chất khí được xác định bằng các thông số trạng thái: áp suất p, thể tích V và nhiệt độ tuyệt đối T.
Câu 17: Có 7 gam khí Nitơ ở điều kiện tiêu chuẩn. Người ta nén đẳng nhiệt khối khí này tới áp suất 133 cmHg thì thể tích của khối khí bây giờ là bao nhiêu?
- A
- B
- C
- D
Số mol nitơ là nN2=mM=728=0,25 mol → V1=0,25.22,4=5,6ℓ.
Thể tích này ứng với áp suất thường p1=1atm=760mmHg
Theo định luật Bôi-lơ Ma-ri-ốt: p1V1=p2V2 → V2=p1V1p2=760.5,61330=3,2ℓ=3,2dm3.
Câu 18: Công thức nào sau đây diễn tả định luật Boylo – Mariotte?
- A
- B
- C
- D
Định luật Boylo – Mariotte: Ở nhiệt độ không đổi thì tích của áp suất p và thể tích V của một lượng khí xác định là một hằng số pV=const
Câu 19: Đặc điểm nào sau đây không phải là đặc điểm của quá trình đẳng nhiệt ?
- A
- B
- C
- D
Nhiệt độ của khối khí không đổi nên không thể xảy ra nhiệt độ khối khí tăng thì áp suất tăng. Còn khi nhiệt độ không đổi thì áp suất và thể tích tỉ lệ nghịch.
Câu 20: Quá trình đẳng nhiệt là quá trình chất khí có
- A
- B
- C
- D
Quá trình đẳng nhiệt là quá trình có nhiệt độ không đổi.