Tứ giác
Lý thuyết về Tứ giác
Định nghĩa: Tứ giác ABCD là hình gồm bốn đoạn thẳng AB,BC,CD,DA trong đó bất kỳ hai đoạn thẳng nào cũng không nằm trên một đường thẳng.
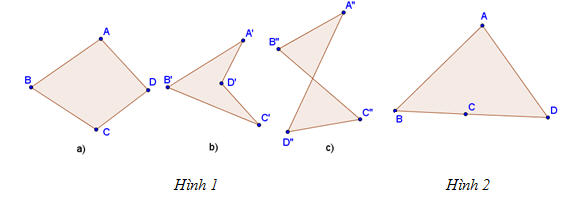
Trong hình 1, các hình ABCD, A′B′C′D′, A"B"C"D" đều là các tứ giác, hình 2 không là tứ giác
Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì một cạnh nào của tứ giác.
Hình 1a là tứ giác lồi ABCD, các hình 1b và 1c đều không là tứ giác lồi.
Khi nói đến tứ giác mà không chú thích gì thêm, ta hiểu đó là tứ giác lồi.
Định lí: Tổng các góc của một tứ giác bằng 360∘.
Bài tập tự luyện có đáp án
Câu 1: Cho tứ giác ABCD có ˆA=65∘;ˆB=117∘;ˆC=71∘. Số đo góc ngoài tại đỉnh D bằng
- A
- B
- C
- D
Sử dụng tính chất Tổng các góc trong của một tứ giác bằng 360∘ ta tìm được ˆD=360∘−65∘−117∘−71∘=107∘
Khi đó góc ngoài ˆD1=180∘−107∘=73∘
Câu 2: Cho hình vẽ dưới đây, chọn khẳng định sai. 
- A
- B
- C
- D
Từ hình vẽ ta thấy các điểm E,H nằm bên ngoài tứ giác và điểm F nằm bên
trong tứ giác ABCD .
Câu 3: Cho hình vẽ sau. Chọn câu sai. 
- A
- B
- C
- D
Tứ giác ABCD có các cặp góc đối nhau là ˆA;ˆC và ˆB;ˆD còn ˆA;ˆB là hai góc kề nhau.
Câu 4: Tứ giác ABCD có: ˆA+ˆB=100∘,ˆA+ˆC=ˆD+15∘,2ˆA+ˆB=ˆC. Khẳng định nào trong các khẳng định sau là đúng?
- A
- B
- C
- D
Kết hợp với điều kiện: Tổng các góc trong của một tứ giác bằng 360∘ ta tính được các số đo góc: ˆA=25∘,ˆB=75∘,ˆC=125∘,ˆD=135∘.
Câu 5:  Tính giá trị của x trong hình vẽ
Tính giá trị của x trong hình vẽ
 Tính giá trị của x trong hình vẽ
Tính giá trị của x trong hình vẽ- A
- B
- C
- D
Sử dụng tính chất: Tổng các góc trong của một tứ giác bằng 360∘ ta tính được x=36∘
Câu 6: Cho tứ giác ABCD, trong đó có ˆA+ˆC=140∘. Tổng ˆB+ˆD bằng
- A
- B
- C
- D
Áp dụng tính chất Tổng các góc trong của một tứ giác bằng 360∘
Câu 7: Số đo các góc của tứ giác ABCD theo tỷ lệ: ˆA:ˆB:ˆC:ˆD=4:3:2:1. Số đo các góc theo thứ tự đó là
- A
- B
- C
- D
Áp dụng tính chất tổng các góc trong của một tứ giác bằng 360∘ ta tính được giá trị các góc là 144∘;108∘;72∘;36∘
Câu 8: Hãy chọn câu sai.
- A
- B
- C
- D
Dựa vào định lý: Tổng các góc của một tứ giác bằng 3600 .
Xem thêm các bài tiếp theo bên dưới