Một số hệ thức về cạnh và đường cao trong tam giác vuông
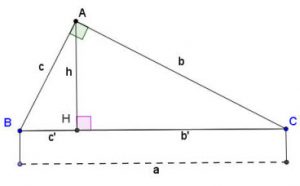
Lý thuyết về Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Trong một tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền: b2=a⋅b′;c2=a⋅c′.
- Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền: h2=b′c′.
- Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng: b⋅c=a⋅h.
- Trong một tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông: 1h2=1b2+1c2.
Bài tập tự luyện có đáp án
Câu 1: Cho tam giác ABC vuông tại A , đường cao AH . Biết AB:AC=3:4 và AB+AC=21cm . Độ dài các đoạn AH,BH,CH lần lượt là
- A
- B
- C
- D
Ta có AB=9;AC=12;BC=15
⇒AH.BC=AB.AC⇒AH=AB.ACBC=12.915=7,2
AB2=BH.BC⇒BH=AB2BC=8115=5,4
⇒CH=BC−BH=15−5,4=9,6
Vậy AH=7,2;BH=5,4;CH=9,6 .
Câu 2: Cho tam giác ABC vuông tại A , đường cao AH . Gọi D và E lần lượt là hình chiếu vuông góc của H trên AB,AC (hình vẽ) 
Tỉ số AB3AC3 bằng
Tỉ số AB3AC3 bằng
- A
- B
- C
- D
Tam giác vuông AHB có BH2=BD.AB⇒BD=BH2AB
Tam giác vuông AHC có HC2=AC.EC⇒EC=HC2AC
Từ đó BDEC=HB2AB:HC2AC2=HB2HC2.ACAB
mà dễ dàng ta có AB2AC2=HBHC nên BDEC=AB4AC4.ACAB⇔BDEC=AB3AC3 .
Câu 3: Tìm x,y trong hình vẽ sau 
- A
- B
- C
- D
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có
AB2=BH.BC⇔BH=AB2BC=14420=7,2⇒CH=BC−BH=20−7,2=12,8 .
Vậy x=7,2;y=12,8 .
Câu 4: Cho tam giác ABC vuông tại A , đường cao AH . Cho biết BH=9cm,CH=16cm . Gọi D,E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và AC . Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M,N . (hình vẽ) 
Diện tích tứ giác DENM bằng
Diện tích tứ giác DENM bằng
- A
- B
- C
- D
Vì DM⊥DE,EN⊥DE⇒DM∥EN;ˆD=ˆE=90∘ nên DENM là hình thang vuông
Ta có DM=BH2=4,5;EN=CH2=8;DE=12
Nên SDENM=(DM+DN).DE2=(4,5+8).122=75cm2 .
Câu 5: Tính x trong hình vẽ sau


- A
- B
- C
- D
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có
1MD2=1MN2+1MP2⇒164=1x2+1x2⇒164=2x2⇒x2=128⇔x=8√2 .
Vậy x=8√2 .
Câu 6: Cho tam giác ABC vuông tại A , đường cao AH . Biết AB:AC=5:12 và AB+AC=34cm . Tính các cạnh của tam giác ABC .
- A
- B
- C
- D
Theo giả thiết: AB:AC=5:12 .
Suy ra AB5=AC12=AB+AC5+12=3417=2 . Do đó AB=5.2=10(cm);AC=2.12=24(cm) .
Tam giác ABC vuông tại A , theo định lý Pytago ta có BC2=AB2+AC2=102+242=676 , suy ra BC=26cm .
Câu 7: Trong một tam giác vuông, nghịch đảo bình phương đường cao ứng với cạnh huyền bằng
- A
- B
- C
- D
Trong một tam giác vuông, nghịch đảo bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo bình phương hai cạnh góc vuông.
Câu 8: Trong hình bên, độ dài BH bằng:


- A
- B
- C
- D
Ta có: Theo định lý Pytago trong tam giác ABC ta có
BC2=AB2+AC2=32+42=25BC=√25=5cm .
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ABC đường cao AH ta có:
AB2=BC.BH⇒BH=AB2BC=325=1,8
Câu 9: Tính x trong hình vẽ sau 
- A
- B
- C
- D
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có
1AH2=1AB2+1AC2⇒AH=AB.AC√AB2+AC2=15.20√152+202=12 .
Vậy x=12 .
Câu 10: Cho tam giác ABC vuông tại A , đường cao AH . Gọi D và E lần lượt là hình chiếu vuông góc của H trên AB,AC (hình vẽ) 
Tỉ số AB2AC2 bằng
Tỉ số AB2AC2 bằng
- A
- B
- C
- D
Xét tam giác vuông ABC có AH là đường cao nên AB2=BH.BC;AC2=CH.BC
Nên AB2AC2=BH.BCCH.BC=HBHC
Câu 11: Tính x,y trong hình vẽ sau 
- A
- B
- C
- D
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có
AH2=BH.CH⇒AH2=2.5⇒AH=√10 .
Áp dụng định lý Pytago cho tam giác vuông AHB;AHC ta có
AB=√AH2+HB2=√10+4=√14;AC=√AH2+HC2=√10+25=√35
Vậy x=√14;y=√35 .
Câu 12: Tính x,y trong hình vẽ sau 
- A
- B
- C
- D
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có
AB2=BH.BC⇔BH=AB2BC=10016=6,25⇒CH=BC−BH=16−6,25=9,75 .
Vậy x=6,25;y=9,75 .
Câu 13: Cho tam giác CDE nhọn, đường cao CH . Gọi M,N theo thứ tự là hình chiếu của H lên CD,DE . (hình vẽ) 
Tam giác CMN đồng dạng với tam giác nào dưới đây?
Tam giác CMN đồng dạng với tam giác nào dưới đây?
- A
- B
- C
- D
Câu trước ta có CM.CD=CN.CE⇔CMCN=CECD
Xét ΔCMN và ΔCED có ˆC chung và CMCN=CECD nên ΔCMN∼ΔCED (c – g – c)
Câu 14: Cho tam giác ABC vuông tại A , đường cao AH . Biết AB:AC=3:4 và AB+AC=21cm . Độ dài các cạnh của tam giác ABC lần lượt là
- A
- B
- C
- D
Theo giả thiết: AB:AC=3:4
Suy ra AB3=AC4=AB+AC3+4=3 . Do đó AB=3.3=9(cm);AC=3.4=12(cm) .
Tam giác ABC vuông tại A , theo định lý Pytago ta có BC2=AB2+AC2=92+122=225 , suy ra BC=15cm .
Câu 15: Cho hình vẽ bên, tam giác ABC vuông tại A ,cạnh AB=10cm ,đường cao AH=8cm . Độ dài cạnh BC bằng:


- A
- B
- C
- D
Theo pitago, tam giác vuông AHB ⇒BH=6cm
Theo hệ thức lượng trongtam giác có: AH2=BH.HC⇒HC=323⇒BC=503cm .
Câu 16: Trên hình 1.2 ta có:


- A
- B
- C
- D
Áp dụng hệ thức b2=b′.a ta có 92=x.15 suy ra x=5,4 và y=15−5,4=9,6 .
Câu 17: Cho tam giác CDE nhọn, đường cao CH . Gọi M,N theo thứ tự là hình chiếu của H lên CD,DE . (hình vẽ) 
Tích CD.CM bằng
Tích CD.CM bằng
- A
- B
- C
- D
Tam giác CHD vuông tại H , ta có CH2=CM.CD
Tam giác CHE vuông tại H , ta có CH2=CN.CE
Nên CM.CD=CN.CE
Câu 18: Cho tam giác ABC vuông tại A , đường cao AH . Cho biết BH=9cm,CH=16cm . Gọi D,E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và AC . Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M,N . (hình vẽ) 
Độ dài đoạn thẳng DE bằng
Độ dài đoạn thẳng DE bằng
- A
- B
- C
- D
Tứ giác AEHD là hình chữ nhật vì ˆA=ˆE=ˆD=90∘ nên DE=AH
Xét ΔABC vuông tại A có AH2=HB.HC=16.9=144⇒AH=12
Nên DE=12cm .
Câu 19: Tìm x,y trong hình vẽ sau


- A
- B
- C
- D
Theo định lý Pytago ta có BC2=AB2+AC2⇔BC2=100⇔BC=10 .
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có AB2=BH.BC⇒BH=AB2BC=6210=3,6 hay x=3,6⇒CH=BC−BH=10−3,6=6,4 hay y=6,4 .
Vậy x=3,6;y=6,4 .
Câu 20: Tìm x,y trong hình vẽ sau 
- A
- B
- C
- D
Theo định lý Pytago ta có BC2=AB2+AC2⇔BC2=74⇔BC=√74 .
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có AH.BC=AB.AC⇔AH=AB.ACBC=5.7√74=35√7474 .
Vậy x=35√7474;y=√74 .
Câu 21: Cho tam giác ABC vuông tại A , đường cao AH . Cho biết BH=4cm,CH=9cm . Gọi D,E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và AC . Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M,N . (hình vẽ) 
Diện tích tứ giác DENM bằng
Diện tích tứ giác DENM bằng
- A
- B
- C
- D
Vì DM⊥DE,EN⊥DE⇒DM∥EN;ˆD=ˆE=90∘ nên DENM là hình thang vuông
Ta có DM=BH2=2;EN=CH2=4,5;DE=6
Nên SDENM=(DM+DN).DE2=19,5cm2 .
Câu 22: Cho tam giác ABC vuông tại A , đường cao AH . Cho biết BH=9cm,CH=16cm . Gọi D,E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và AC . Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M,N . (hình vẽ) 
Độ dài đoạn thẳng DE bằng
Độ dài đoạn thẳng DE bằng
- A
- B
- C
- D
Tứ giác AEHD là hình chữ nhật vì ˆA=ˆE=ˆD=90∘ nên DE=AH
Xét ΔABC vuông tại A có AH2=HB.HC=9.16=144⇒AH=12
Nên DE=12cm .
Câu 23: Tính x trong hình vẽ sau 
- A
- B
- C
- D
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có
1MD2=1MN2+1MP2⇒164=1x2+1x2⇔164=2x2⇒x2=128⇔x=8√2 .
Vậy x=8√2 .
Câu 24: Tính x trong hình vẽ sau (làm tròn đến chữ số thập phân thứ hai) 
- A
- B
- C
- D
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ABC ta có
1AH2=1AB2+1AC2⇔1AH2=AB2+AC2AB2.AC2⇔AH2=AB2.AC2AB2+AC2
⇒AH=AB.AC√AB2+AC2=15.20√152+202=12 .
Vậy x=12 .
Câu 25: Cho tam giác ABC vuông tại A , đường cao AH . Biết AB:AC=5:12 và AB+AC=34cm . Tính độ dài các đoạn AH,BH,CH (làm tròn đến chữ số thập phân thứ hai)
- A
- B
- C
- D
Dễ dàng ta có AB=10;AC=24;BC=26 .
⇒AH.BC=AB.AC⇒AH=AB.ACBC=10.2426≈9,23 ;
AB2=BH.BC⇒BH=AB2BC=10213=10013≈7,69 .
⇒CH=BC−BH=26−7,69=18,31 .
Vậy AH≈9,23;BH≈7,69;CH≈18,31 .
Câu 26: Cho tam giác ABC vuông tại C. Trong các hệ thức dưới đây hệ thức nào đúng ?
- A
- B
- C
- D
Câu 27: Tính x,y trong hình vẽ sau 
- A
- B
- C
- D
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có
AH2=BH.CH⇒AH2=1.4⇒AH=2 .
Áp dụng định lý Pytago cho tam giác vuông AHB;AHC ta có
AB=√AH2+HB2;AC=√AH2+HC2=2√5 .
Vậy x=√5;y=2√5 .
Câu 28: Cho tam giác ABC vuông tại A , chiều cao AH và AB=5;AC=12 . Đặt BC=y;AH=x . Giá trị của x,y lần lượt là
- A
- B
- C
- D
Theo định lý Pytago ta có BC2=AB2+AC2⇔BC2=169⇔BC=13 .
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có
AH.BC=AB.AC⇔AH=AB.ACBC=5.1213=6013 .
Vậy x=6013;y=13 .
Câu 29: Tính x,y trong hình vẽ sau 
- A
- B
- C
- D
Theo định lý Pytago ta có BC2=AB2+AC2⇔BC2=25⇔BC=5 .
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có
AB2=BH.BC⇒BH=AB2BC=325=1,8 hay x=1,8 .
⇒CH=BC−BH=5−1,8=3,2 hay y=3,2 .
Vậy x=1,8;y=3,2 .