Đối xứng trục
Lý thuyết về Đối xứng trục
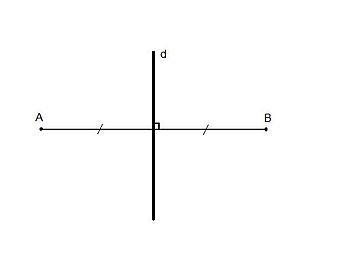
Hai điểm đối xứng qua một đường thẳng.
Định nghĩa: Hai điểm gọi là đối xứng với nhau qua đường thẳng dd nếu dd là đường trung trực của đoạn thẳng nối hai điểm đó.
Qui ước: Nếu điểm B nằm trên đường thẳng dd thì điểm đối xứng với B qua đường thẳng dd cũng là điểm B.
Hai hình đối xứng qua một đường thẳng.
Định nghĩa: Hai hình gọi là đối xứng với nhau qua đường thẳng dd nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng dd và ngược lại. Đường thẳng dd gọi là trục đối xứng của hai hình đó.
Hình có trục đối xứng.
Định nghĩa: Đường thẳng dd gọi là trục đối xứng của hình HH nếu điểm đối xứng với mỗi điểm thuộc hình HH qua đường thẳng dd cũng thuộc hình HH. Ta nói rằng hình HH có trục đối xứng.
Định lí: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang đó.
Bài tập tự luyện có đáp án
Câu 1: Chọn phát biểu đúng trong các phát biểu sau
- A
- B
- C
- D
Hai điểm A,BA,B gọi là đối xứng với nhau qua đường thẳng dd nếu dd là đường trung trực của đoạn thẳng ABAB.
Câu 2: Hãy chọn câu sai.
- A
- B
- C
- D
Vì hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.
Câu 3: Cho hình vẽ. Hãy chọn câu đúng. 
- A
- B
- C
- D
Từ hình vẽ ta có đường thẳng dd là đường trung trực của đoạn thẳng AKAK nên điểm đối xứng với AA qua đường thẳng dd là KK .
Câu 4: Khẳng định sai là
- A
- B
- C
- D
Không có khái niệm hai đường thẳng bằng nhau.
Câu 5: Từ hình vẽ bên dưới, hãy chọn câu sai trong các câu dưới đây. 
- A
- B
- C
- D
Từ hình vẽ ta có A và A′ đối xứng nhau qua đường thẳng m ; B và B′ đối xứng nhau qua đường thẳng m ; C và C′ đối xứng nhau qua đường thẳng m .
Suy ra hai đoạn thẳng EB và E′B′ đối xứng nhau qua m .
Hai đoạn thẳng DB và D′B′ đối xứng nhau qua m .
Hai tam giác DEB và D′E′B′ đối xứng nhau qua m .
Hai đoạn thẳng DE và D′E′ đối xứng nhau qua m .
Câu 6: Cho tam giác ABC cân tại B, các đường trung tuyến AA′,BB′,CC′, Trục đối xứng của tam giác ABC là
- A
- B
- C
- D
Do tam giác ABC cân tại B nên đường trung tuyến BB′ đồng thời là đường trung trực. Do đó BB′ là trục đối xứng của tam giác ABC.
Câu 7: Cho tam giác ABC, trong đó AB=11cm, AC=15cm, BC=13cm. Vẽ hình đối xứng với tam giác ABC qua trục là cạnh BC. Chu vi tứ giác tạo thành là
- A
- B
- C
- D
Gọi A′ là điểm đối xứng với A qua BC. Khi đó chu vi tứ giác tạo thành là:
AB+BA′+A′C+CA=2(AB+AC)=52cm.
Câu 8: Hãy chọn câu đúng.
- A
- B
- C
- D
+ Hình thang cân có trục đối xứng là đường thẳng đi qua trung điểm hai đáy nên hình thang cân có một trục đối xứng.
+ Tam giác cân có một trục đối xứng là đường trung trực hạ từ đỉnh cân.
+ Tam giác thường thì không có trục đối xứng.
+ Tam giác đều có ba trục đối xứng là ba đường trung trực của tam giác.
Câu 9: Chọn khẳng định sai trong các khẳng định sau:
- A
- B
- C
- D
Câu 10: Khẳng định sai là
- A
- B
- C
- D
Tam giác đều có ba trục đối xứng là 3 đường cao đi qua mỗi đỉnh của tam giác.
Tam giác cân chỉ có duy nhất một trục đối xứng là đường cao đi qua đỉnh cân của nó.
Đường tròn có vô số trục đối xứng là các đường thẳng đi qua tâm đường tròn.
Câu 11: Chọn khẳng định đúng trong các khẳng định sau
- A
- B
- C
- D
+ Hình thang cân có trục đối xứng là đường thẳng đi qua trung điểm hai đáy nên hình thang cân có một trục đối xứng.
+ Tam giác cân có một trục đối xứng là đường trung trực hạ từ đỉnh cân.
+ Tam giác thường thì không có trục đối xứng.
+ Tam giác đều có ba trục đối xứng là ba đường trung trực của tam giác nên.
Câu 12: Cho đoạn thẳng AB có độ dài 3cm và đường thẳng d . Đoạn thẳng A′B′ đối xứng với AB qua d . Độ dài đoạn thẳng A′B′ là
- A
- B
- C
- D
Vì đoạn thẳng A′B′ đối xứng với AB qua d nên A′B′=AB=3cm .
Câu 13: Cho tam giác ABC cân tại B , các đường trung tuyến AA′,BB′,CC′ . Trục đối xứng của tam giác ABC là
- A
- B
- C
- D
Do tam giác ABC cân tại B , nên đường trung tuyến BB′ đồng thời là đường trung trực.
Do đó BB′ là trục đối xứng của tam giác ABC .
Câu 14: Hãy chọn câu đúng. Trục đối xứng của hình thang cân là
- A
- B
- C
- D
Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.