Diện tích tam giác
Lý thuyết về Diện tích tam giác
1. Định lý
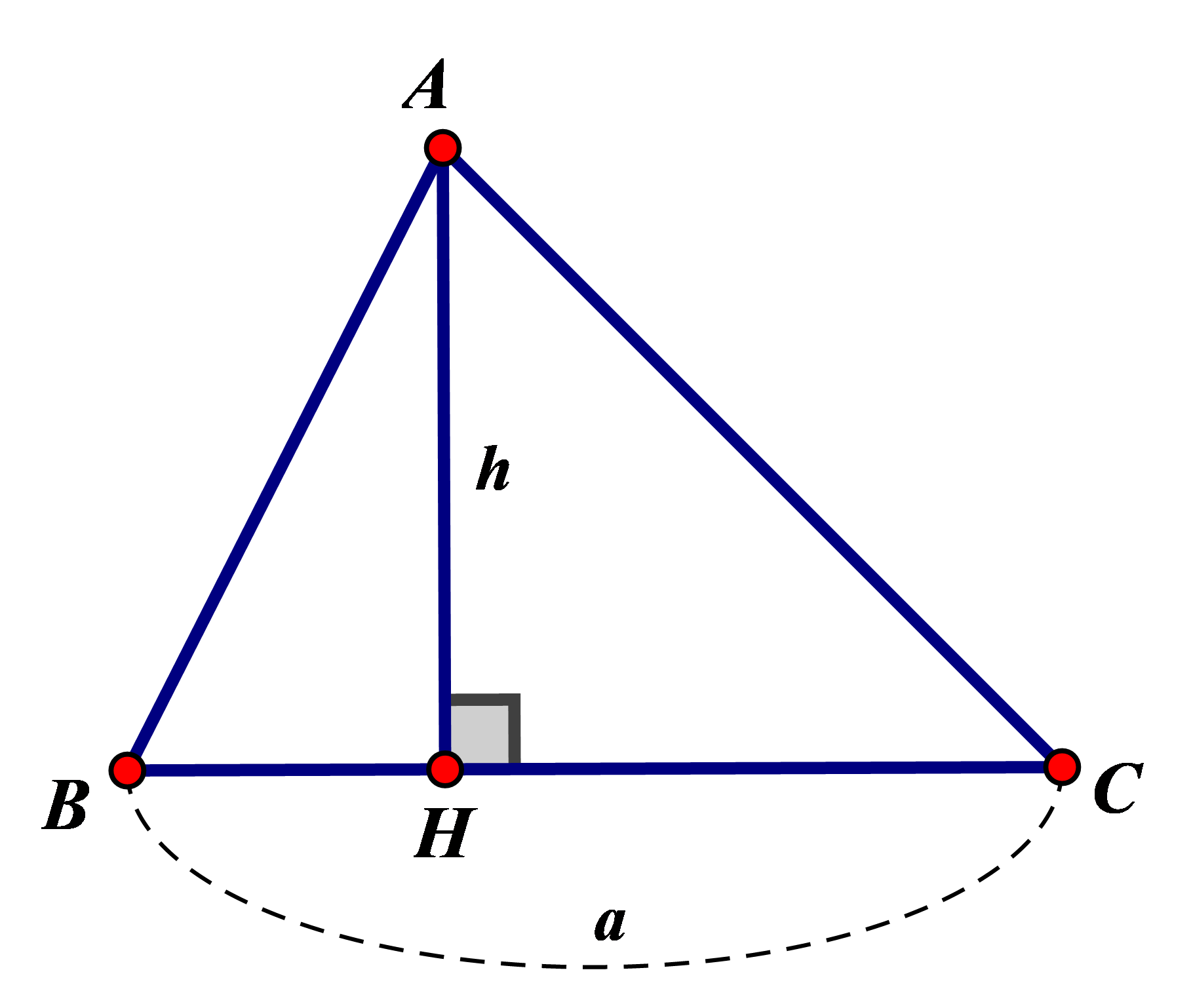
Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.
S=12ah
2. Hệ quả
Diện tích tam giác vuông bằng nửa tỉ số hai cạnh góc vuông.
S=12bc
Bài tập tự luyện có đáp án
Câu 1:  Diện tích hình vẽ với các thông số tương ứng như hình bên là
Diện tích hình vẽ với các thông số tương ứng như hình bên là
 Diện tích hình vẽ với các thông số tương ứng như hình bên là
Diện tích hình vẽ với các thông số tương ứng như hình bên là- A
- B
- C
- D
Ta có
SABCD=abSEAB=12(c−a)b⇒SEABCD=ab+12(c−a)b=12(c+a)b
Câu 2: Hai cạnh của một tam giác có độ dài là 4cm và 6cm. Diện tích của tam giác không thể nhận giá trị nào trong các giá trị sau đây
- A
- B
- C
- D
Giả sử hai cạnh của tam giác là 4 cm và 6 cm.
Chiều cao tương ứng của hai tam giác là h và k.
Ta có: S1=12.4.h ; S2=12.6.k
h và k là đường cao tương ứng với cạnh đáy là 4 và 6.
Theo tính chất của đường vuông góc và đường xiên thì {h≤4h≤6
Suy ra diện tích của tam giác S≤18
Câu 3: Diện tích của một tam giác đều có cạnh bằng a là
- A
- B
- C
- D

Gọi H là chân đường cao từ A, ta có HC=a2
Khi đó AH=√a2−a24=a√32
⇒SABC=12AH.BC=12.a√32.a=a2√34
Câu 4: Cho tam giác ABC và đường trung tuyến AM, AH là đường cao ( H thuộc BC). Lấy N là trung điểm của AC. Khẳng định đúng là
- A
- B
- C
- D

Kẻ đường cao AH.
Ta có SABM=12AH.BM;SACM=12AH.CM
Mà BM=CM (vì AM là trung tuyến)
Vậy SAMB=SAMC
Câu 5: Cho tam giác AOB vuông tại O với đường cao OM. Khi đó ta có
- A
- B
- C
- D

Ta có diện tích ΔAOB qua đường cao OM và cạnh đáy AB: SOAB=12OM.AB
Ta có tính diện tích ΔAOB vuông với hai cạnh góc vuông OA, OB là: SOAB=12OA.OB
Suy ra AB.OM=OA.OB
Câu 6: Cho tam giác ABC, biết AB=2AC . Tỉ số hai đường cao xuất phát từ đỉnh B và C bằng
- A
- B
- C
- D

Gọi BH và CK là 2 đường cao trong tam giác ABC
Ta có: SABC=12AB.CK=12AC.BH
Suy ra: AB.CK=AC.BH⇒BHCK=ABAC
Mà AB=2AC(gt)⇒BKCH=2ACAC=2 .
Câu 7: Diện tích của một tam giác cân có cạnh đáy bằng a và cạnh bên bằng b là
- A
- B
- C
- D

Ta có HC=a2⇒AH2=AC2−HC2=b2−a24
⇒AH=√b2−a24=12√4b2−a2⇒SABC=12AH.BC=12.12√4b2−a2.a=14a√4b2−a2
Câu 8: Trong hình bên, số tam giác có diện tích bằng diện tích tam giác SAOB là


- A
- B
- C
- D
Ta có: OA=OB=OC=OD (tính chất hình chữ nhật)
ΔOAB=ΔOCD(c.g.c)⇒SOAB=SOCD(1)
ΔOAD=ΔOBC(c.g.c)⇒SOAD=SOBC(2)
Kẻ AH⊥BD ; SOAD=12AH.OD ; SOAB=12AH.OB
Suy ra: SOAD=SOAB(3)
Từ (1), (2) và (3) ⇒SOAB=SOBC=SOCD=SODA
Vậy có 3 tam giác trong hình có diện tích bằng diện tích tam giác OAB .
Câu 9: Cho tam giác ABC có đáy BC cố định và đỉnh A di động trên đoạn thẳng DE , với DE qua A và DE song song với BC. Khi đó khẳng định nào sau đây là sai?
- A
- B
- C
- D
Tam giác ABC có cạnh đáy BC không đổi, chiều cao AH là khoảng cách giữa 2 đường thẳng song song không đổi.
Vậy điểm A thay đổi trên DE//AB thì SABC không đổi.
Nên SABC<SDBC là sai.
Câu 10: Cho tam giác ABC;AM là đường trung tuyến. Biết diện tích của ΔABC bằng 60cm2 . Diện tích của tam giác AMC là
- A
- B
- C
- D
Kẻ AH⊥BC tại H .
Ta có SABC=12AH.BC;SAMC=12AH.MC
Mà AM là đường trung tuyến nên M là trung điểm của BC⇒BC=2AM Từ đó SABC=12AH.BC=12AH.2MC=2SAMC
Suy ra SAMC=12SABC=12.60=30cm2 .
Vậy SAMC=30cm2 .
Câu 11: Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S′ là diện tích của tam giác DBC. Khi đó SS′ bằng
- A
- B
- C
- D

Hai ΔABC và ΔDBC có chung canh đáy BC nên ta có:
SABC=12AH.BC=S
SDBC=12DK.BC=S′
⇒SS′=AHDK
Câu 12: Cho tam giác ABC , lấy M thuộc BC sao cho BM=3CM . Hãy chọn câu sai.
- A
- B
- C
- D
Kẻ AH⊥BC tại H .
Mà BM=3CM⇒BM=34BC;CM=14BC
Khi đó ta có
SABM=12.AH.BM=12AH.34BC=34.(12AH.BC)=34SABC
SAMB=12.AH.MB=12AH.3MC=3.(12AH.MC)=3SAMC
SABC=12.AH.BC=12AH.4MC=4SAMC⇒SABC=4SAMC⇔SAMC=14SABC.
Xem thêm các bài tiếp theo bên dưới