Chia đa thức một biến đã sắp xếp
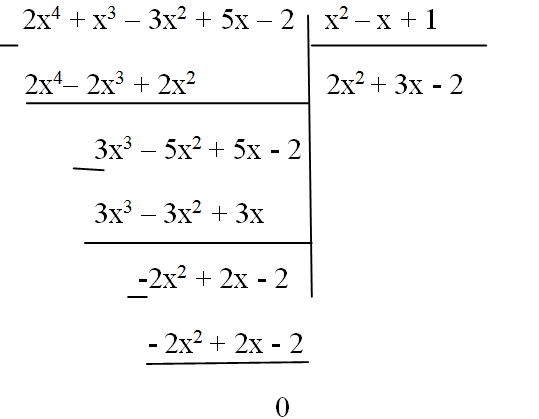
Lý thuyết về Chia đa thức một biến đã sắp xếp
Phương pháp:
Ta trình bày phép chia tương tự như cách chia các số tự nhiên. Với hai đa thức A và B của một biến, B≠0 tồn tại duy nhất hai đa thức Q và R sao cho:
A=B.Q+R, với R=0 hoặc bậc bé hơn bậc của 1
– Nếu R=0, ta được phép chia hết.
– Nếu R≠0, ta được phép chia có dư.
Ví dụ
Làm tính chia: (2x4+x3−3x2+5x−2):(x2−x+1)
Bài tập tự luyện có đáp án
Câu 1: Số dư của phép chia (2x4−10x3+3x2−3x+2):(2x2+1) là
- A
- B
- C
- D
Ta có

Khi đó 2x4−10x3+3x2−3x+2=(2x2+1)(x2−5x+1)+2x+1
Vậy phần dư của phép chia là : 2x+1
Câu 2: Tổng bình phương các giá trị của a để đa thức x4−3x3+5x2−3x+a2 chia hết cho đa thức x2−3x+4 là
- A
- B
- C
- D
Ta có
x4−3x3+5x2−3x+a2x4−3x3+4x2|_x2−3x+4_x2+1x2−3x+a2x2−3x+4_a2−4
Như vậy để là phép chia hết thì a2−4=0⇔a=±2
Câu 3: Kết quả của phép chia (2x4+x3−5x2−3x−3):(x2−3) là
- A
- B
- C
- D
Cách 1 :

Cách 2:
2x4+x3−5x2−3x−3=2x4−6x2+x3−3x+x2−3=2x2(x2−3)+x(x2−3)+x2−3=(x2−3)(2x2+x+1)⇒(2x4+x3−5x2−3x−3):(x2−3)=2x2+x+1
Câu 4: Phép chia đa thức 3x5+5x4−1 cho đa thức x2+x+1 được thương là
- A
- B
- C
- D

Đa thức thương là 3x3+2x2−5x+3 .
Câu 5: Phép chia đa thức 2x4−3x3+3x−2 cho đa thức x2−1 được số dư là
- A
- B
- C
- D

Vậy đa thức dư là R=0 .
Câu 6: Kết quả của phép chia (x5−x2−3x4+3x+5x3−5):(x2−3x+5) là
- A
- B
- C
- D
Ta có

Câu 7: Phần dư của phép chia đa thức x4−2x3+x2−3x+1 cho đa thức x2+1 có hệ số tự do là
- A
- B
- C
- D

Đa thức dư là −x+1 có hệ số tự do là 1 .
Câu 8: Kết quả của phép chia (6x2 +13x−5):(2x+5) bằng
- A
- B
- C
- D
Cách 1 làm tính chia:

Cách 2:
6x2 +13x−5=6x2+15x−2x−5=3x(3x+5)−(2x+5)=(2x+5)(3x−1)⇒(6x2 +13x−5):(2x+5)=3x−1
Câu 9: Kết quả của phép chia (x3 −3x2+x−3):(x−3) là
- A
- B
- C
- D
Cách 1:

Cách 2:
x3 −3x2+x−3=x2(x−3)+x−3=(x2+1)(x−3)⇒(x3 −3x2+x−3):(x−3)=x2+1
Câu 10: Kết quả của phép chia (x3+27):(x+3) là
- A
- B
- C
- D
Ta có x3+27=(x+3)(x2−3x+9)
Khi đó (x3+27):(x+3)=x2−3x+9
Câu 11: Kết quả của phép chia (12x2−14x+3−6x3+x4):(1−4x+x2) là
- A
- B
- C
- D

Xem thêm các bài tiếp theo bên dưới