Các trường hợp đồng dạng của tam giác vuông
Lý thuyết về Các trường hợp đồng dạng của tam giác vuông
Các trường hợp đồng dạng của tam giác vuông
Từ các trường hợp đồng dạng của tam giác đã học suy ra: Hai tam giác vuông đồng dạng nếu có một trong các điều kiện:
+ Một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia;
+ Hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia.
Định lý:
Trường hợp đồng dạng đặc biệt: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đồng dạng.
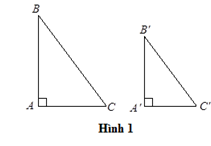
Nếu ΔABC và ΔA′B′C′ có ˆA=^A′=90o và ABA′B′=BCB′C′ (hình 1) thì ΔABC∼ΔA′B′C′ (g.g)
Tỉ số đường cao, tỉ số diện tích của hai tam giác đồng dạng
Nếu hai tam giác đồng dạng thì:
+ Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng;
+ Tỉ số hai diện tích bằng bình phương tỉ số đồng dạng.
Bài tập tự luyện có đáp án
Câu 1: Cho tam giác ABC vuông tại A , đường cao AH . Biểu thức nào sau đây đúng?
- A
- B
- C
- D

Xét ΔAHB và ΔCHA có
^AHB=^CHA=900
^ABH=^CAH (cùng phụ với ^BAH )
Suy ra ΔAHB∼ΔCHA ⇒AHCH=HBHA⇒AH2=HB.HC
Câu 2: Cho tam giác ABC đường cao AH đồng dạng với tam giác A′B′C′ đường cao A′H′ theo tỉ số đồng dạng là 12 . Tỉ số AHA′H′ bằng
- A
- B
- C
- D
Tỉ số đường cao tương ứng của 2 tam giác đồng dạng thì bằng tỉ số đồng dạng ⇒AHA′H′=12
Câu 3: Tam giác ABC vuông tại A có đường cao AH . Cho biết AB=3cm AC=4cm . Tính độ dài các đoạn thẳng HA,HB .
- A
- B
- C
- D
Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
AB2+AC2=BC2⇔32+42=BC2⇔BC2=25⇒BC=5cm
Xét 2 tam giác vuông ABC và HBA có: ˆB chung
⇒ΔABC∽ΔHBA(g−g) ⇒ABHB=BCBA⇒HB=AB2BC=325=1,8cm
Mặt khác:
ABHB=ACHA⇒HA=AC.HBAB=4.1,83=2,4cm
Nên HA=2,4cm;HB=1,8cm .
Câu 4: Cho tam giác ABC cân tại A , AC=20cm , BC=24cm các đường cao AD và CE cắt nhau ở H . Tính độ dài HD .
- A
- B
- C
- D
Tam giác ABC cân tại A nên BD=DC=BC2=242=12(cm)
Theo định lý Py-ta-go, ta có AD2=AC2−DC2=202−122=162 nên AD=16cm
Xét ΔCDH và ΔADB có
^CDH=^ADB=90o .
^C1=^A1 (cùng phụ với ˆB ).
Do đó ΔCDH∽ΔADB(g.g)
Nên HDBD=HCAB=CDAD , tức là HD12=HC20=1216=34
Suy ra HD=9cm .
Câu 5: Cho tam giác ABC vuông ở A,AB=6cm,AC=8cm đường cao AH , đường phân giác BD . Gọi I là giao điểm của AH và BD . Chọn khẳng định đúng.
- A
- B
- C
- D
Xét 2 tam giác vuông ABD và HBI có:
^ABD=^HBI ( BD là tia phân giác của góc B )
⇒ΔABD∽ΔHBI(g−g) ⇒ABHB=BDBI⇔AB.BI=BD.HB.
Câu 6: Cho tam giác ABC vuông tại A , đường cao AH . Biểu thức nào sau đây đúng?
- A
- B
- C
- D

Xét tam giác ΔAHC và ΔBAC có
^AHC=^BAC=900
ˆC chung
⇒ΔAHC∼ΔBAC ⇒ACBC=HCAC⇒AC2=BC.HC
Câu 7: Cho hình vẽ sau.
 Có bao nhiêu cặp tam giác đồng dạng ?
Có bao nhiêu cặp tam giác đồng dạng ?
 Có bao nhiêu cặp tam giác đồng dạng ?
Có bao nhiêu cặp tam giác đồng dạng ?
- A
- B
- C
- D

Ta có ΔABH∼ΔCAH , ΔABH∼ΔCBA , ΔAHC∼ΔBAC
Câu 8: Cho tam giác ABC vuông ở A , đường cao AH . Tích HB.HC bằng
- A
- B
- C
- D
Ta có: ^HAB+^HAC=^BAC=900
Mà: ^HBA+^HAB=900 (2 góc phụ nhau)
⇒^HAC=^HBA
Xét 2 tam giác vuông AHB và CHA ta có ^HAC=^HBA (cmt)
⇒ΔAHB∽ΔCHA(g−g)⇒AHCH=HBHA⇔AH2=HB.HC .
Câu 9: Cho tam giác ABC vuông ở A , đường cao AH . Cho BH=9cm,HC=16cm . Tính diện tích tam giác ABC .
- A
- B
- C
- D
Với BH=9cm,HC=16cm .
⇒BC=BH+HC=9+16=25cm
Ta có: ^HAB+^HAC=^BAC=900
Mà: ^HBA+^HAB=900 (2 góc phụ nhau)
⇒^HAC=^HBA
Xét 2 tam giác vuông AHB và CHA ta có ^HAC=^HBA (cmt)
⇒ΔAHB∽ΔCHA(g−g)⇒AHCH=HBHA⇔AH2=HB.HC .
Ta có: AH2=HB.HC
⇒AH2=9.16=144⇒AH=12cm
Nên diện tích tam giác ABC là . SABC=12AH.BC=12.12.25=150cm2 .
Xem thêm các bài tiếp theo bên dưới