Đồ thị của hàm số y = ax^2 (a ≠ 0)
Lý thuyết về Đồ thị của hàm số y = ax^2 (a ≠ 0)
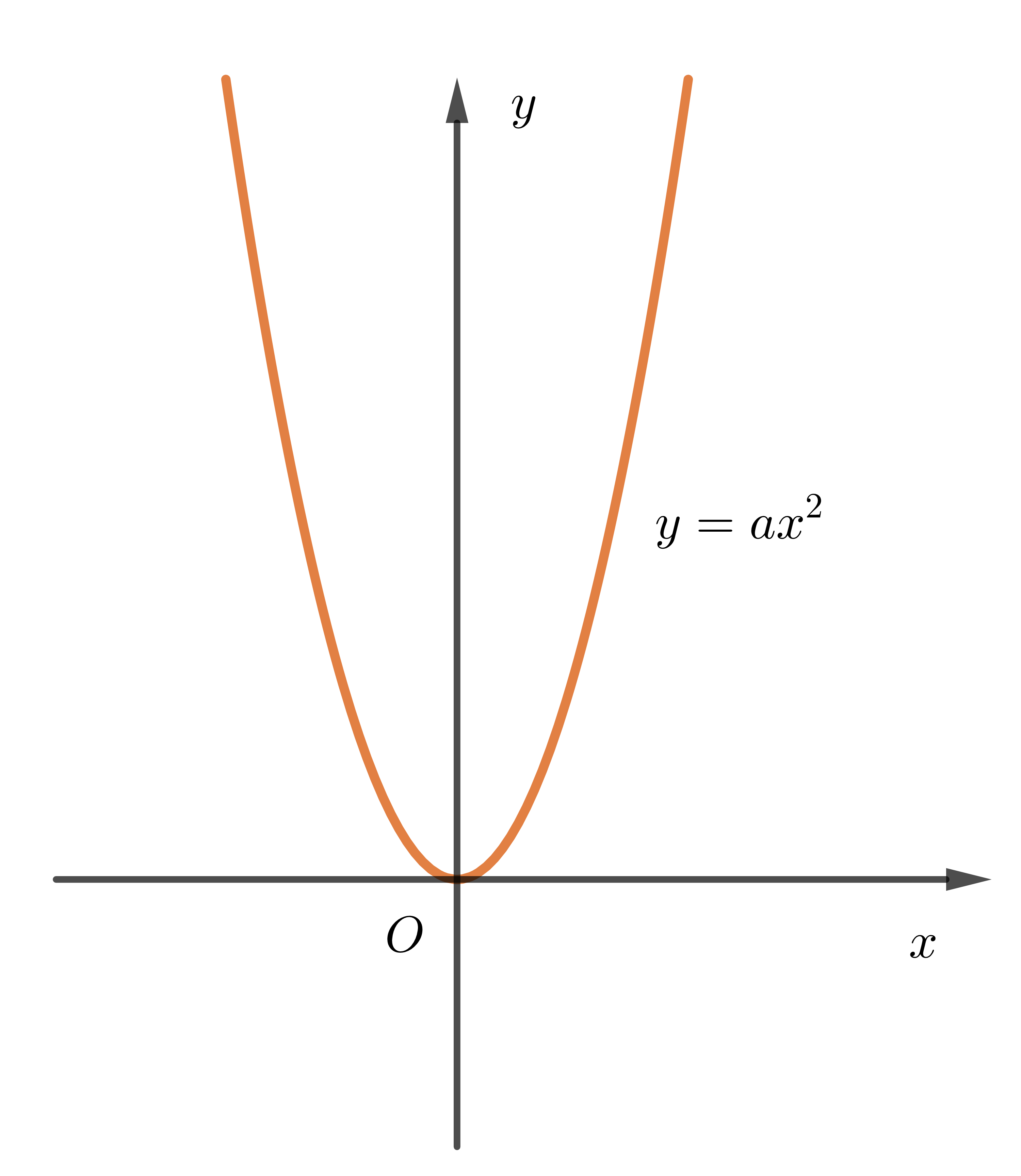
1. Đồ thị hàm số $y = ax^2 (a ≠ 0)$
Đồ thị của hàm số $y = ax^2 (a ≠ 0)$ là một đường cong đi qua gốc tọa độ và nhận trục $Oy$ làm trục đối xứng. Đường cong đó được gọi là một parabol với đỉnh $O.$
– Nếu $a > 0$ thì đồ thị nằm phía trên trục hoành, $O$ là điểm thấp nhất của đồ thị.
– Nếu $a < 0$ thì đồ thị nằm phía dưới trục hoành, $O$ là điểm cao nhất của đồ thị.
2. Cách vẽ đồ thị $y = ax^2 (a ≠ 0)$
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ 5 đến 7 giá trị) tương ứng giữa x và y.
Bước 3: Vẽ đồ thị và kết luận.
Bài tập tự luyện có đáp án
Câu 1: Hình vẽ dưới đây là của đồ thị hàm số nào?
- A
- B
- C
- D
Từ hình vẽ suy ra $ a < 0 $ nên chỉ có hàm số $ y=-{{x}^{2}} $ và $ y=-2{{x}^{2}} $ thỏa mãn $ a < 0 $
Vì đồ thị đi qua điểm có tọa độ $ \left( 1;-1 \right) $ nên chỉ có hàm số $ y=-{{x}^{2}} $ thỏa mãn.
Vậy hàm số cần tìm là $ y=-{{x}^{2}} $ .
Câu 2: Cho hàm số $ y={{x}^{2}} $ có đồ thị là parabol $ \left( P \right) $ . Điểm nào dưới đây không thuộc $ \left( P \right) $ ?
- A
- B
- C
- D
Thay lần lượt tọa độ các điểm vào hàm số $ y={{x}^{2}} $ ta được:
+) $ 0={{0}^{2}} $ (đúng) nên điểm $ O $ thuộc $ \left( P \right) $ .
+) $ 1={{\left( -1 \right)}^{2}} $ (đúng) nên điểm $ N $ thuộc $ \left( P \right) $ .
+) $ -1={{\left( -1 \right)}^{2}} $ (sai) nên điểm $ M $ không thuộc $ \left( P \right) $ .
+) $ 1={{1}^{2}} $ (đúng) nên điểm $ Q $ thuộc $ \left( P \right) $ .
Vậy chỉ có điểm $ M $ không thuộc $ \left( P \right) $ .
Câu 3: Cho hàm số $ :y=\left( m-1 \right){{x}^{2}} $ với $ m\ne 1 $ . Tìm $ m $ để đồ thị hàm số đi qua $ \left( -1;2 \right) $ là:
- A
- B
- C
- D
Thay $ x=-1;y=2 $ vào hàm số ta được: $ 2=\left( m-1 \right).1\Leftrightarrow m-1=2\Leftrightarrow m=3 $ (thỏa mãn).
Câu 4: Cho hàm số $ y=m{{x}^{2}} $ (m là tham số). Giá trị của m để đồ thị hàm số đi qua điểm A $ (-2;6) $ là
- A
- B
- C
- D
Để đồ thị hàm số $ y=m{{x}^{2}} $ đi qua điểm A $ (-2;6)\Leftrightarrow 6=m{{(-2)}^{2}}\Leftrightarrow m=\dfrac{3}{2} $
Câu 5: Kết luận nào sau đây là sai khi nói về đồ thị của hàm số $ y=a{{x}^{2}}\,\, $ với $ a\ne 0 $ ?
- A
- B
- C
- D
Đồ thị của hàm số $ y=a{{x}^{2}}\left( a\ne 0 \right) $ là một parabol đi qua gốc tọa độ O, nhận Oy làm trục đối xứng (O là đỉnh của parabol).
- Nếu $ a > 0 $ thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
- Nếu $ a < 0 $ thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.
Vậy kết luận sai cần chọn là:
" Với $ a > 0 $ đồ thị nằm phía trên trục hoành và $ O $ là điểm cao nhất của đồ thị".
Câu 6: Trong các hàm số dưới đây, hàm số nào có đồ thị nằm phía trên trục hoành?
- A
- B
- C
- D
Hàm số $ y=0,05{{x}^{2}} $ có $ a=0,05 > 0 $ nên đồ thị nằm phía trên trục hoành.
Câu 7: Biết đồ thị hàm số $ y=m{{x}^{2}}\,\left( m\ne 0 \right) $ đi qua điểm $ A\left( 2;-1 \right) $ . Giá trị của $ m $ là
- A
- B
- C
- D
Do điểm $ A\left( 2;-1 \right) $ thuộc đồ thị hàm số $ y=m{{x}^{2}}\,\left( m\ne 0 \right) $ nên thay $ x=2 $ và $ y=-1 $ vào $ y=m{{x}^{2}} $ ta được $ -1=m{{.2}^{2}}\Leftrightarrow m=\dfrac{-1}{4} $ (thỏa mãn). Vậy $ m=\dfrac{-1}{4} $ .
Câu 8: Cho đồ thị hàm số $(C): y=a{{x}^{2}}\left( a > 0 \right)$. Kết luận nào dưới đây là không đúng?
- A
- B
- C
- D
Đồ thị hàm số $ y=a{{x}^{2}}\left( a > 0 \right) $ luôn đi qua điểm $ O\left( 0;0 \right) $ , nằm trên trục hoành và có bề lõm hướng lên trên.
Do đó, kết luận đồ thị hàm số đó luôn nằm trên trục tung là sai.
Xem thêm các bài tiếp theo bên dưới