Tính chất tia phân giác của một góc
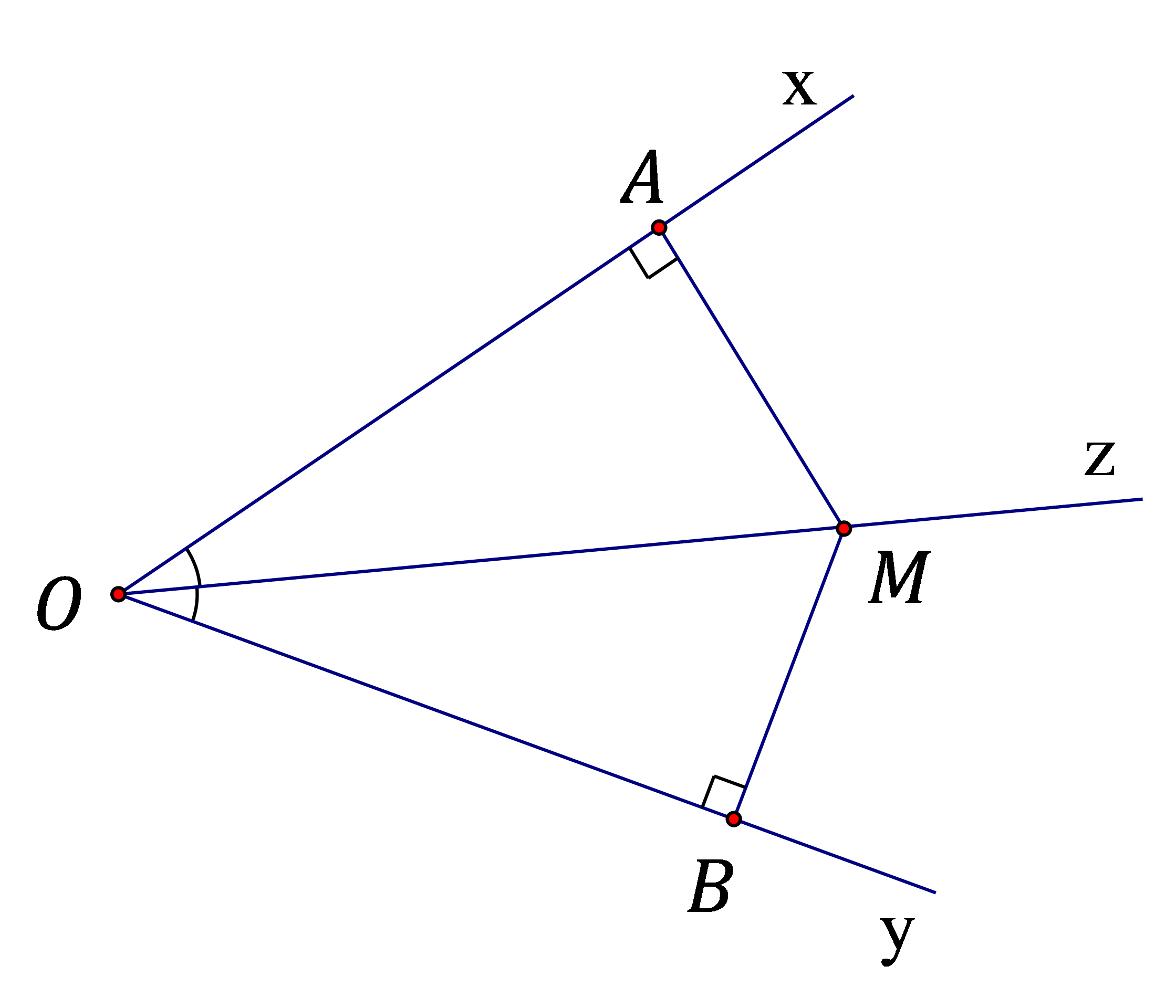
Lý thuyết về Tính chất tia phân giác của một góc
1. Định lí 1 (định lí thuận)
Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó
Cụ thể: Góc $\widehat{xOy}$, tia phân giác $Oz$, $M\in Oz$. $A$ và $B$ là hình chiếu của $M$ lên \[Ox\] và $Oy$. Khi đó: $MA=MB$
2. Định lí 2 (định lí đảo)
Điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên phân giác của góc đó.
Cụ thể: Góc $\widehat{xOy}$, điểm $M$ nằm bên trong góc $\widehat{xOy}$.$A$ và $B$ là hình chiếu của $M$ lên \[Ox\] và $Oy$. Nếu$MA=MB$ thì $M$ nằm trên tia phân giác của góc $\widehat{xOy}$
Bài tập tự luyện có đáp án
Câu 1: Cho hình vẽ bên dưới:
 Chọn khẳng định sai.
Chọn khẳng định sai.
 Chọn khẳng định sai.
Chọn khẳng định sai.
- A
- B
- C
- D
Ta có: B nằm trong góc xAy, $ BM\bot Ax,BI\bot Ay,BM=BI. $
Do đó: B nằm trên tia phân giác của $ \widehat{xAy}. $
Chứng minh tương tự: C, D nằm trên tia phân giác của $ \widehat{xAy}. $
Vậy ba điểm B, C, D thẳng hàng.
Câu 2: Cho tam giác $ ABC $ vuông tại $ A $ , đường phân giác $ BE $ . Kẻ $ ED\bot BC\,\,\left( D\in BC \right) $ . Khẳng định nào dưới đây là sai?
- A
- B
- C
- D
Xét tam giác vuông $ \Delta ABE $ và tam giác vuông $ \Delta DBE $ có
DE là cạnh chung
$ \widehat{BAE}=\widehat{BED}={{90}^{o}} $
$ \widehat{ABE}=\widehat{EBD} $ ( BE là phân giác )
$ \Rightarrow \Delta ABE=\Delta DBE\Rightarrow \left\{ \begin{array}{l} BD=BA \\ EA=ED \end{array} \right. $
Gọi H là giao của BE và AD
Ta dễ dàng cm $ \Delta ABH=\Delta DBH\left( c-g-c \right) $
$ \Rightarrow \widehat{AHB}=\widehat{BHD} $ ( 2 góc tương ứng)
Mà hai góc $ \widehat{AHB};\widehat{BHD} $ ở vị trí kề bù
Nên $ \widehat{AHB}=\widehat{BHD}={{90}^{o}} $
Vậy $ BE\bot AD $ .
Câu 3: Cho tam giác $ ABC $ vuông ở $ C $ , $ \hat{A}={{70}^{0}} $ . Tia phân giác của $ \widehat{CAB} $ cắt $ BC $ tại điểm $ E $ . Từ $ E $ kẻ $ EK\bot AB $ . Số đo của $ \widehat{AEK} $ bằng
- A
- B
- C
- D
Do $ EK\bot AB $ nên $ \widehat{EKA}={{90}^{0}} $
$ AE $ là phân giác của $ \widehat{CAB} $ nên $ \widehat{EAK}=\dfrac{1}{2}\widehat{CAB}={{35}^{0}} $
Xét $ \Delta AKE $ với $ \widehat{EKA}={{90}^{0}} $
Có $ \widehat{AEK}={{90}^{0}}-\widehat{EAK}={{90}^{0}}-{{35}^{0}}={{55}^{0}} $ .
Câu 4: Hai tia phân giác của hai góc kề bù thì hai tia phân giác đó
- A
- B
- C
- D
Ta có 2 góc $ \widehat{xOz} $ và $ \widehat{zOy} $ kề bù; $ Om;\,\,\,On $ là 2 tia phân giác của $ \widehat{xOz} $ và $ \widehat{zOy} $
Nên $ \widehat{mOz}=\dfrac{1}{2}\widehat{xOz} $ và $ \widehat{zOn}=\dfrac{1}{2}\widehat{zOy} $
Vậy $ \widehat{mOn}=\widehat{mOz}+\widehat{zOn}=\dfrac{1}{2}\left( \widehat{xOz}+\widehat{zOy} \right)=\dfrac{1}{2}\widehat{xOy}={{90}^{0}} $ .
Câu 5: Các đường phân giác của góc B và góc C trong tam giác ABC cắt nhau ở H. Cho biết $ \widehat{A}={{80}^{0}} $ , khi đó số đo $ \widehat{BHC} $ là
- A
- B
- C
- D

Ta có: $ \widehat{ABC}+\widehat{ACB}={{180}^{0}}-\widehat{A}={{180}^{0}}-{{80}^{0}}={{100}^{0}}. $
Vì BH và CH lần lượt là tia phân giác của góc B và góc C nên $ \widehat{HBC}+\widehat{HCB}=\dfrac{\widehat{ABC}+\widehat{ACB}}{2}={{50}^{0}}\Rightarrow \widehat{BHC}={{180}^{0}}-{{50}^{0}}={{130}^{0}}. $
Câu 6: Cho $ N $ là điểm nằm trên tia phân giác của góc $ \widehat{xOy} $ . Khoảng cách từ $ N $ đến tia $ Ox $ là 4cm. Khoảng cách từ $ N $ đến tia $ Oy $ là
- A
- B
- C
- D
Từ $ N $ ta kẻ các đoạn $ NA\bot Ox\,\left( A\in Ox \right),\,\,NB\bot \,Oy\,\left( B\in Oy \right) $
Xét tam giác vuông $ \Delta ONA $ và tam giác vuông $ \Delta ONB $ có
$ ON $ là cạnh huyền chung
$ \widehat{NOA}=\widehat{NOB} $
$ \Rightarrow \Delta AON=\Delta BON $ ( ch-gn)
$ \Rightarrow NA=NB $ hai cạnh tương ứng.
Nên $ NA=NB=4 $ cm.
Câu 7: Cho góc xOy là góc tù. Trên nửa mặt phẳng không chứa Oy có bờ là tia Ox, vẽ tia Oz vuông góc với tia Ox. Trên nửa mặt phẳng không chứa tia Ox có bờ là tia Oy, vẽ tia Oz’ vuông góc với Oy. Gọi Ot là tia phân giác của góc xOy, Ot’ là tia đối của tia Ot. Khẳng định nào sau đây là sai ?
Khẳng định nào sau đây là sai ?
- A
- B
- C
- D

Đường thẳng t’Ot chia mặt phẳng thành 2 nửa mặt phẳng, nửa mặt phẳng chứa tia Ox, nửa mặt phẳng chứa tia Oy.
Góc xOy là góc tù, $ \widehat{\text{tOx}}=\dfrac{1}{2}\widehat{xOy} $ (vì Ot là tia phân giác) nên $ \widehat{tOx} $ là góc nhọn.
$ \widehat{xOz}={{90}^{0}} $ nên $ \widehat{tOz} $ là góc tù.
Do đó: tia Oz nằm trên nửa mặt phẳng chứa tia Ox mà bờ là đường tt’.
Vậy khẳng định sai cần chọn là: " $ \widehat{tOz} $ là góc vuông".
Câu 8: Cho tam giác ABC có $ AB < AC. $ Tia phân giác của góc A cắt đường trung trực của BC ở D. Gọi H và K là chân các đường vuông góc kẻ từ D đến các đường thẳng AB và AC.
Chọn khẳng định sai.
- A
- B
- C
- D

Theo tính chất tia phân giác của góc: $ DH=DK. $
Gọi M là trung điểm của BC, ta có: $ \Delta DMB=\Delta DMC\left( c.g.c \right)\Rightarrow DB=DC. $
$ \Rightarrow \Delta DHB=\Delta DKC $ (cạnh huyền – cạnh góc vuông) $ \Rightarrow BH=CK,\widehat{DBH}=\widehat{DCK}. $
Vậy khẳng định sai cần chọn là: " $ DB > DC $ ".
Câu 9: Cho tam giác ABC, kẻ tia phân giác Ax của góc BAC. Tại C kẻ đường thẳng song song với tia Ax, nó cắt tia đối của tia AB tại D. Chọn khẳng định sai.
Chọn khẳng định sai.
- A
- B
- C
- D

Vì Ax là tia phân giác của góc BAC nên $ \widehat{xAB}=\widehat{xAC} $ (1)
$ Ax//CD $ bị cắt bởi đường thẳng AC, hai góc xAC và ACD là hai góc so le trong nên $ \widehat{xAC}=\widehat{ACD} $ (2)
$ \widehat{xAB}=\widehat{ADC} $ (hai góc đồng vị) (3)
Từ (1), (2) và (3) ta có: $ \widehat{xAB}=\widehat{xAC}=\widehat{ACD}=\widehat{ADC}. $
Vậy khẳng định sai cần chọn là: " $ \widehat{BAC}=\widehat{ACD} $ ".
Câu 10: Cho tam giác ABC, K là giao điểm của hai tia phân giác của hai góc ngoài $ \widehat{CBx} $ và $ \widehat{BCy} $ . Kẻ $ KD\bot Bx,KE\bot BC,KF\bot Cy $ (như hình vẽ): 
Chọn khẳng định sai.

Chọn khẳng định sai.
- A
- B
- C
- D
K thuộc tia phân giác của góc CBx và $ KD\bot Bx\,;\,KE\bot BC $ nên $ KD=KE. $ (1)
K thuộc tia phân giác của góc BCy và $ \,KE\bot BC\,;\,KF\bot Cy $ nên $ KE=KF. $ (2)
Từ (1) và (2) $ \Rightarrow KD=KF\Rightarrow $ K thuộc tia phân giác của góc A.
Câu 11: Cho hình vẽ sau, trong đó tia Ot nằm giữa hai tia Ox và Oy, tia Ot’ là tia phân giác của $ \widehat{xOy'} $ .
 Nếu điểm M cách đều hai đường thẳng xx’ và yy’ thì khẳng định nào sau đây là đúng ?
Nếu điểm M cách đều hai đường thẳng xx’ và yy’ thì khẳng định nào sau đây là đúng ?
 Nếu điểm M cách đều hai đường thẳng xx’ và yy’ thì khẳng định nào sau đây là đúng ?
Nếu điểm M cách đều hai đường thẳng xx’ và yy’ thì khẳng định nào sau đây là đúng ?- A
- B
- C
- D
Vì điểm M cách đều hai đường thẳng xx’ và yy’ nên điểm M thuộc tia phân giác của góc tạo bời hai đường thẳng đó.
Mà Ot’ là tia phân giác của $ \widehat{xOy'} $ nên điểm M thuộc tia Ot’ hoặc tia đối của tia Ot’.
Vậy điểm M thuộc đường thẳng Ot’.
Câu 12: Cho tam giác ABC, kẻ tia phân giác Bx của góc B; Bx cắt tia AC tại M. Từ M kẻ đường thẳng song song với AB, nó cắt BC tại N. Từ N kẻ đường thẳng Ny song song với tia Bx. Chọn khẳng định sai.
Chọn khẳng định sai.
- A
- B
- C
- D

Vì Bx là tia phân giác của góc B nên $ \widehat{ABx}=\widehat{xBC}. $
$ MN//BA\Rightarrow \widehat{BMN}=\widehat{ABx} $ (hai góc so le trong) $ \Rightarrow \widehat{xBC}=\widehat{BMN}. $
$ Ny//Bx\Rightarrow \widehat{BMN}=\widehat{MNy} $ (hai góc so le trong), $ \widehat{xBC}=\widehat{yNC} $ (hai góc đồng vị).
Vậy khẳng định sai cần chọn là: " $ \widehat{xBC}=\widehat{MNC} $ ".
Câu 13: Trên hình vẽ sau, điểm nào nằm trên tia phân giác của $ \widehat{xOy}? $ 

- A
- B
- C
- D
Từ hình vẽ ta thấy chỉ có điểm A cách đều hai cạnh của $ \widehat{xOy} $
Do đó: điểm A thuộc tia phân giác của $ \widehat{xOy}. $
Câu 14: Cho hai đường thẳng xx’ và yy’ cắt nhau tại O. Hai tia phân giác Ot và Ot’ của một cặp góc kề bù tạo thành một góc có số đo bằng:
- A
- B
- C
- D

Ot và Ot’ lần lượt là tia phân giác của hai góc kề bù $ \widehat{xOy} $ và $ \widehat{xOy} $ nên ta có:
$ \widehat{xOt}+\widehat{xOt'}=\dfrac{1}{2}\widehat{xOy}+\dfrac{1}{2}\widehat{xOy'}=\dfrac{1}{2}\left( \widehat{xOy}+\widehat{xOy'} \right)=\dfrac{1}{2}{{.180}^{0}}={{90}^{0}}\Rightarrow \widehat{tOt'}={{90}^{0}}. $
Câu 15: Cho tam giác $ ABC $ , có $ \hat{A}={{70}^{0}} $ , $ AD $ là tia phân giác của $ \widehat{A} $ . Từ $ D $ vẽ đường thẳng song song với $ AB $ cắt $ AC $ tại $ M $ . Số đo góc $ \widehat{ADM} $ bằng
- A
- B
- C
- D
Do $ DM\text{//}AB\Rightarrow \widehat{ADM}=\widehat{BAD} $ ( so le trong)
Mà $ AD $ là tia phân giác của $ \widehat{BAC}\Rightarrow \widehat{BAD}=\widehat{DAC}=\dfrac{1}{2}\widehat{BAC} $
Nên $ \widehat{ADM}=\dfrac{1}{2}\widehat{BAC}={{35}^{0}} $ .
Câu 16: Cho $ \Delta ABC $ có $ \hat{B}={{80}^{0}},\,\,\,\hat{C}={{30}^{0}} $ . Tia phân giác của $ \widehat{A} $ cắt $ BC $ ở $ D $ . Số đo góc $ \widehat{ADC} $ bằng
- A
- B
- C
- D
Xét tam giác $ \Delta ABC $
Ta có $ \widehat{A}={{180}^{0}}-\widehat{B}-\widehat{C}={{180}^{0}}-{{80}^{0}}-{{30}^{0}}={{70}^{0}} $
$ AD $ là phân giác của $ \widehat{A}\Rightarrow \widehat{BAD}=\widehat{DAC}=\dfrac{1}{2}\widehat{A}={{35}^{0}} $
Xét tam giác $ \Delta ABD $ có $ \widehat{ADC} $ là góc ngoài đỉnh D.
$ \Rightarrow \widehat{ADC}=\widehat{BAD}+\widehat{ABD}={{35}^{0}}+{{80}^{0}}={{115}^{0}} $ .