Tính chất của hai tiếp tuyến cắt nhau
Lý thuyết về Tính chất của hai tiếp tuyến cắt nhau
1. Định lý hai tiếp tuyến cắt nhau
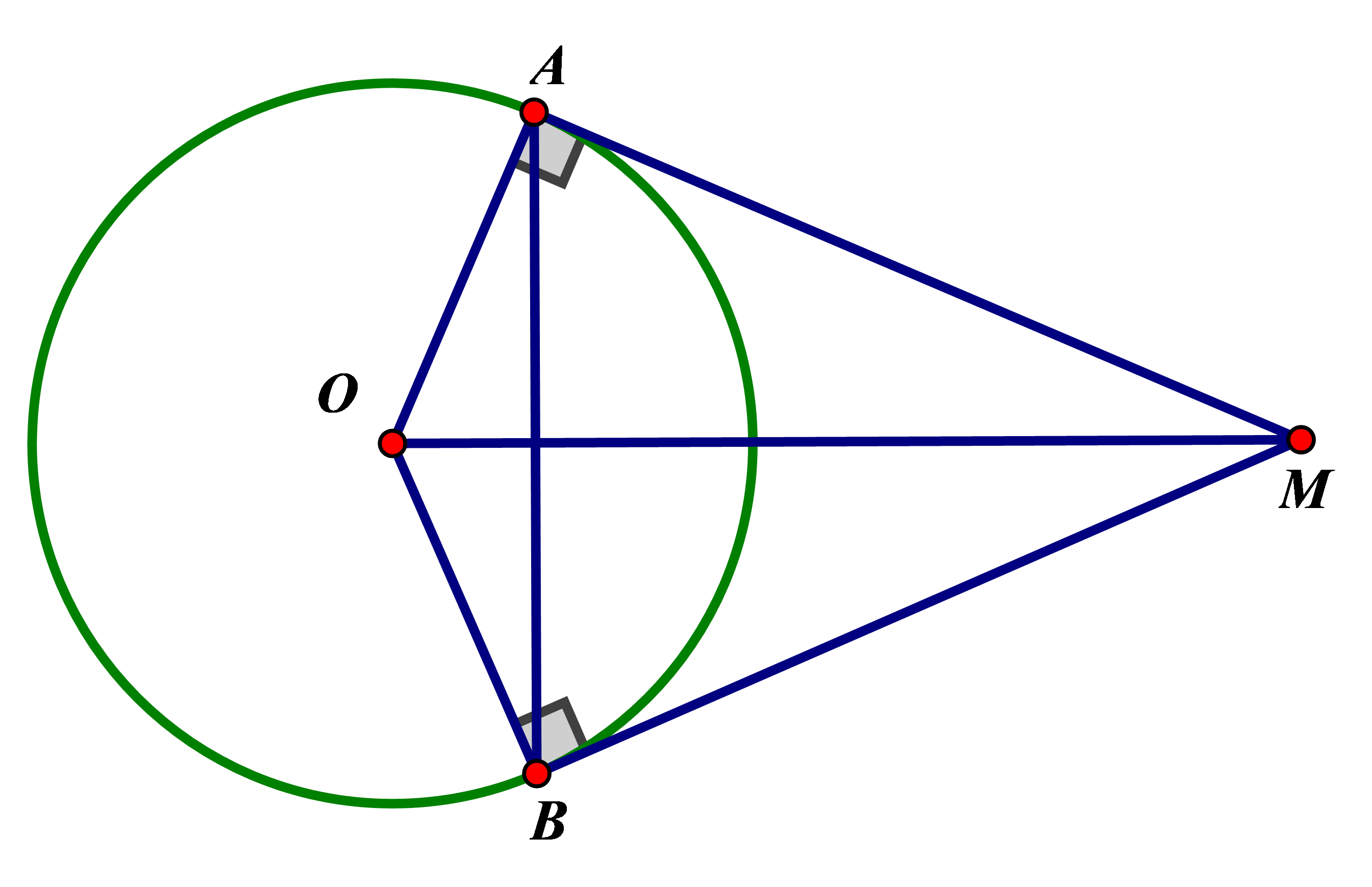
Cho 2 tiếp tuyến tại A,B cắt nhau tại M khi đó ta có
AM=BM
MO là phân giác của góc ^AMB
OM là phân giác của góc ^AOB
OM⊥AB tại trung điểm của AB
2. Đường tròn nội tiếp tam giác
Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với ba cạnh của tam giác
Tâm của đường tròn nội tiếp tam giác là giao điểm của các đường phân giác các góc trong của tam giác.
3. Đường tròn bàng tiếp tam giác
- Đường tròn bàng tiếp tam giác là đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với các phần kéo dài của hai cạnh kia.
- Tâm của đường tròn bàng tiếp trong góc A là giao điểm của hai đường phân giác các góc ngoài tại B và C, giao điểm này cùng nằm trên đường phân giác góc A
- Một tam giác, có ba đường tròn bàng tiếp.
Bài tập tự luyện có đáp án
Câu 1: Hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A.Vẽ đường kính CD của (O) . Khi đó:
- A
- B
- C
- D

Ta có AO⊥BC (*).
Xét tam giác BCD có DC là đường kính của (O) và B∈(O) nên ΔBDC vuông tại B hay BD⊥BC(∗∗)
Từ (*) và (**) suy ra BD//AO .
Mà AO và AC cắt nhau nên BD và AC không thể song song.
Câu 2: Cho đường tròn (O) . Từ một điểm M ở ngoài (O) , vẽ hai tiếp tuyến MA và MB sao cho góc AMB bằng 60∘ . Biết chu vi tam giác MAB là 24cm , tính độ dài bán kính đường tròn.
- A
- B
- C
- D
Xét (O) có MA=MB (tính chất hai tiếp tuyến cắt nhau) mà ^AMB=60∘ nên ΔMAB đều suy ra chu vi ΔMAB là MA+MB+AB=3AB⇒AB=8cm=MA=MB
Lại có ^AMO=12^AMB=30∘ (tính chất 2 tiếp tuyến cắt nhau)
Xét tam giác vuông MAO có sin^AMO=OAMA⇒OA=MA.sin30∘=4cm
Câu 3: Cho hai tiếp tuyến của một đường tròn cắt nhau tại một điểm. Chọn khẳng định sai.
- A
- B
- C
- D
Nếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì:
- Điểm đó cách đều hai tiếp điểm.
- Tia kẻ từ điểm đó đi qua tâm là tia phân giác của các góc tạo bởi hai tiếp tuyến.
- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm.
Câu 4: Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại I . Đường thẳng qua I và vuông góc với IA cắt OB tại K . Chọn khẳng định đúng.
- A
- B
- C
- D
Xét (O) có IA,IB là hai tiếp tuyến cắt nhau tại I nên ^AOI=^KOI .
Mà OA//KI (vì cùng vuông góc với AI ) nên ^KIO=^IOA (hai góc ở vị trí so le trong)
Từ đó ^KOI=^KIO suy ra ΔKOI cân tại K⇒KI=KO .
Câu 5: Cho tam giác đều ABC nội tiếp đường tròn bán kính 1cm. Diện tích của tam giác ABC bằng:
- A
- B
- C
- D

AO=1(cm) .
⇒AD=32AO=32 (cm)
⇒AB=AD√32=√3 (cm)
⇒SABC=12AD.BC=12.√3.32=3√34 (cm2)
Câu 6: Cho đường tròn (O) , bán kính OA . Dây CD là đường trung trực của OA . Tứ giác OCAD là hình gì?
- A
- B
- C
- D
Gọi H là giao của OA và CD .
Xét (O) có OA⊥CD nên H là trung điểm của CD .
Xét tứ giác OCAD có hai đường chéo OA và CD vuông góc với nhau và giao nhau tại trung điểm H mỗi đường nên OCAD là hình thoi.
Câu 7: Hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A . Biết OB=3cm ; OA=5cm . Chọn khẳng định sai.
- A
- B
- C
- D
Xét (O) có AB,AC là hai tiếp tuyến cắt nhau tại A nên
AB=AC;^CAO=^BAO;^BOA=^COA .
Xét ΔABO vuông tại B có OB=3cm;OA=5cm , theo định lý Pytago ta có:
AB=√OA2−OB2=√52−32=4cm .
Nên AC=AB=4cm .
Xét tam giác ABO vuông tại B có sin^ABO=ABOA=45 .
Mà ^BOA=^COA nên sin^COA=45 .
Câu 8: Cho nửa đường tròn tâm O , đường kính AB=10cm . Vẽ các tiếp tuyến Ax,By với nửa đường tròn cùng phía đối với AB . Từ điểm M trên nửa đường tròn ( M khác A,B ) vẽ tiếp tuyến với nửa đường tròn, cắt Ax và By lần lượt tại C và D , biết OD=8cm . Tính AC và BD .
- A
- B
- C
- D
Áp dụng định lý Pytago cho tam giác BDO ta có BD=√OD2−OB2=√82−52=√39cm .
Mà MD=BD;MC=AC (tính chất hai tiếp tuyến cắt nhau) nên MD=√39cm .
Dễ thấy MC.MD=25⇒MC=25MD=25√39=25√3939 nên AC=MC=25√3939
Vậy BD=√39;AC=25√3939 .
Câu 9: Cho tam giác ABC cân tại A nội tiếp đường tròn (O) . Gọi D là trung điểm cạnh AC , tiếp tuyến của đường tròn (O) tại A cắt tia BD tại E . Chọn khẳng định đúng.
- A
- B
- C
- D
Vì tam giác ABC cân tại A có O là tâm đường tròn ngoại tiếp nên đường thẳng AO⊥BC .
Lại có AO⊥AE (tính chất tiếp tuyến) nên AE//BC .
Câu 10: Cho đường tròn (O;R) và điểm A nằm ngoài (O) . Từ A kẻ hai tiếp tuyến AB,AC với (O) ( B,C là các tiếp điểm). Gọi H là giao điểm của OA và BC . Lấy D đối xứng với B qua O . Gọi E là giao điểm của đoạn thẳng AD với (O) ( E không trùng với D ). Chọn khẳng định đúng.
- A
- B
- C
- D
+ Ta có AB,AC là hai tiếp tuyến của (O)⇒^OBA=^OCA=90∘
⇒B,C cùng thuộc đường tròn đường kính OA
⇒A,B,O,C cùng thuộc một đường tròn đường kính OA .
+ Ta có AB,AC là hai tiếp tuyến của (O) cắt nhau tại A
⇒AB=AC và AO là phân giác ^BAC (tính chất 2 tiếp tuyến cắt nhau)
⇒ΔABC là tam giác cân tại A
⇒AO vừa là phân giác ^BAC vừa là đường trung trực của BC (tính chất tam giác cân).
Câu 11: Cho đường tròn (O);(O′) cắt nhau tại A,B trong đó O′∈(O) . Kẻ đường kính O′OC của đường tròn (O) . Chọn khẳng định sai.
- A
- B
- C
- D
Xét đường tròn (O) có O′C là đường kính, suy ra ^CBO′=^CAO′=90∘ hay CB⊥O′B tại B và AC⊥AO′ tại A .
Do đó AB,BC là hai tiếp tuyến của (O′) nên AC=CB (tính chất hai tiếp tuyến cắt nhau)
Câu 12: Cho tam giác ABC cân tại A nội tiếp đường tròn (O) . Gọi D là trung điểm cạnh AC , tiếp tuyến của đường tròn (O) tại A cắt tia BD tại E . Tứ giác ABCE là hình gì?
- A
- B
- C
- D
Vì AE//BC nên ^EAC=^ACB (hai góc ở vị trí so le trong), lại có ^ADE=^BDC (đối đỉnh) và AD=DC .
Nên ΔADE=ΔCDB (g – c – g)
⇒AE=BC
Tứ giác AECB có AE=BC;AE//BC nên AECB là hình bình hành.
Câu 13: Độ dài mỗi cạnh của tam giác đều ngoại tiếp đường tròn (O; r) bằng:
- A
- B
- C
- D

OF=r=13AF⇒AF=3r=AB√32⇒AB=2√3r
Câu 14: Mỗi tam giác có bao nhiêu đường tròn bàng tiếp?
- A
- B
- C
- D
Đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với phần kéo dài của hai cạnh còn lại gọi là đường tròn bàng tiếp tam giác.
Với một tam giác có ba đường tròn bàng tiếp.
Câu 15: Cho tam giác ABC có AB=3,AC=4,BC=5 . Khẳng định nào sau đây đúng?
- A
- B
- C
- D
BC2=AB2+AC2 ⇒ΔABC vuông ở A . ⇒AB⊥AC ⇒ AC là tiếp tuyến của đường tròn (B;BA)
Câu 16: Hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A. Chọn khẳng định sai?
- A
- B
- C
- D

Gọi H là giao của BC với AO.
Xét (O) có hai tiếp tuyến tại B và C cắt nhau tại A nên AB=AC (tính chất).
Lại có OB=OC nên AO là trung trực của đoạn BC hay AO⊥BC tại H là trung điểm của BC .
Ta chưa thể kết luận được H có là trung điểm của AO hay không.
Câu 17: Cho đường tròn (O) . Từ một điểm M ở ngoài (O) , vẽ hai tiếp tuyến MA và MB sao cho góc AMB bằng 120∘ . Biết chu vi tam giác MAB là 6(3+2√3) cm, tính độ dài dây AB .
- A
- B
- C
- D
Xét (O) có MA=MB;^AMO=^BMO (tính chất hai tiếp tuyến bằng nhau)
Nên ^AMO=60∘ . Xét tam giác vuông AOM có AM=AO.cot^AMO=R√33 nên MA=MB=R√33 .
Lại có ^AOB+^AMB=180∘⇒^AOB=60∘ suy ra ΔAOB là tam giác đều
⇒AB=OB=OA=R
Chu vi tam giác MAB là MA+MB+AB=R√33+R√33+R=6(3+2√3)
⇔R(3+2√33)=6(3+2√3)⇒R=18cm nên AB=18cm .
Câu 18: Cho đường tròn (O) , bán kính OA . Dây CD là đường trung trực của OA . Kẻ tiếp tuyến với đường tròn tại C , tiếp tuyến này cắt đường thẳng OA tại I . Biết OA=R . Tính CI theo R .
- A
- B
- C
- D
Xét tam giác COA có OC=OA=R và OC=AC
(do OCAD là hình thoi) nên ΔCOA là tam giác đều ⇒^COI=60∘ .
Xét tam giác vuông OCI có CI=OC.tan60∘=R√3 .
Vậy CI=R√3 .
Câu 19: Cho tam giác ABC cân tại A,I là tâm đường tròn nội tiếp, K là tâm đường tròn bàng tiếp trong góc A . Gọi O là trung điểm của IK . Tâm của đường tròn đi qua bốn điểm B,I,C,K là
- A
- B
- C
- D
Vì tam giác ABC cân tại A nên I;K∈ đường thẳng AH với { H } =BC∩AI
Ta có ^HCI=12^HCA;^KCH=12^xCH
⇒^ICK=^ICH+^HCK=12(^ACH+^HCx)=90∘
Tương tự ta cũng có ^IBK=90∘
Xét hai tam giác vuông ICK và IBK có OI=OK=OB=OC=IK2
Nên bốn điểm B;I;C;K nằm trên đường tròn (O;IK2)
Câu 20: Cho đường tròn (O), dây AB khác đường kính. Qua O kẻ đường vuông góc với AB, cắt tiếp tuyến tại A của đường tròn tại C. Gọi I là giao điểm của AB và OC, biết bán kính của đường tròn bằng 15cm,AB=24cm . Khẳng định nào sau đây sai?
- A
- B
- C
- D

Do OI vuông góc với AB nên I là trung điểm của AB
Suy ra, OC là trung trực của AB
Ta có: ΔOAC=ΔOBC (c.c.c)
⇒^OBC=900
⇒OB⊥BC
Nên BC là tiếp tuyến của (O)
AI=AB2=12cm , OI=√AO2−AI2=9cm , AO2=OI.OC⇒OC=AO2OI=25cm.
Câu 21: Hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A . Chọn khẳng định sai.
- A
- B
- C
- D
Gọi H là giao của BC với AO .
Xét (O) có hai tiếp tuyến tại B và C cắt nhau tại A nên AB=AC (tính chất).
Lại có OB=OC nên AO là đường trung trực của đoạn BC hay AO⊥BC tại H là trung điểm của BC .
Ta chưa kết luận được H có là trung điểm của AO hay không.
Câu 22: Cho đường tròn (O;R) và điểm A nằm ngoài (O) . Từ A kẻ hai tiếp tuyến AB,AC với (O) ( B,C là các tiếp điểm). Gọi H là giao điểm của OA và BC . Lấy D đối xứng với B qua O . Gọi E là giao điểm của đoạn thẳng AD với (O) ( E không trùng với D ). Tỉ số DEBE bằng
- A
- B
- C
- D
Ta có D đối xứng với B qua O⇒BD là đường kính của (O) mà E∈(O)⇒^BED=90∘
Xét ΔBED và ΔABD có ^BED=^ABD=90∘,ˆD chung
⇒ΔBED∽ΔABD(gg)⇒DEBE=BDBA .
Câu 23: Hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A . Vẽ đường kính CD của (O) . Khi đó
- A
- B
- C
- D
Gọi H là giao của BC với AO .
Xét (O) có hai tiếp tuyến tại B và C cắt nhau tại A nên AB=AC (tính chất).
Lại có OB=OC nên AO là đường trung trực của đoạn BC hay AO⊥BC(∗) tại H là trung điểm của BC .
Xét tam giác BCD có DC là đường kính của (O) và B∈(O) nên ΔBDC vuông tại B hay BD⊥BC (∗∗)
Từ (*) và (**) suy ra BD//AO .
Mà AO và AC cắt nhau nên BD và AC không thể song song.
Câu 24: Tâm đường tròn nội tiếp của tam giác là
- A
- B
- C
- D
Tâm đường tròn nội tiếp của tam giác là giao của ba đường phân giác góc trong tam giác