Tiếp tuyến chung của 2 đường tròn
Lý thuyết về Tiếp tuyến chung của 2 đường tròn
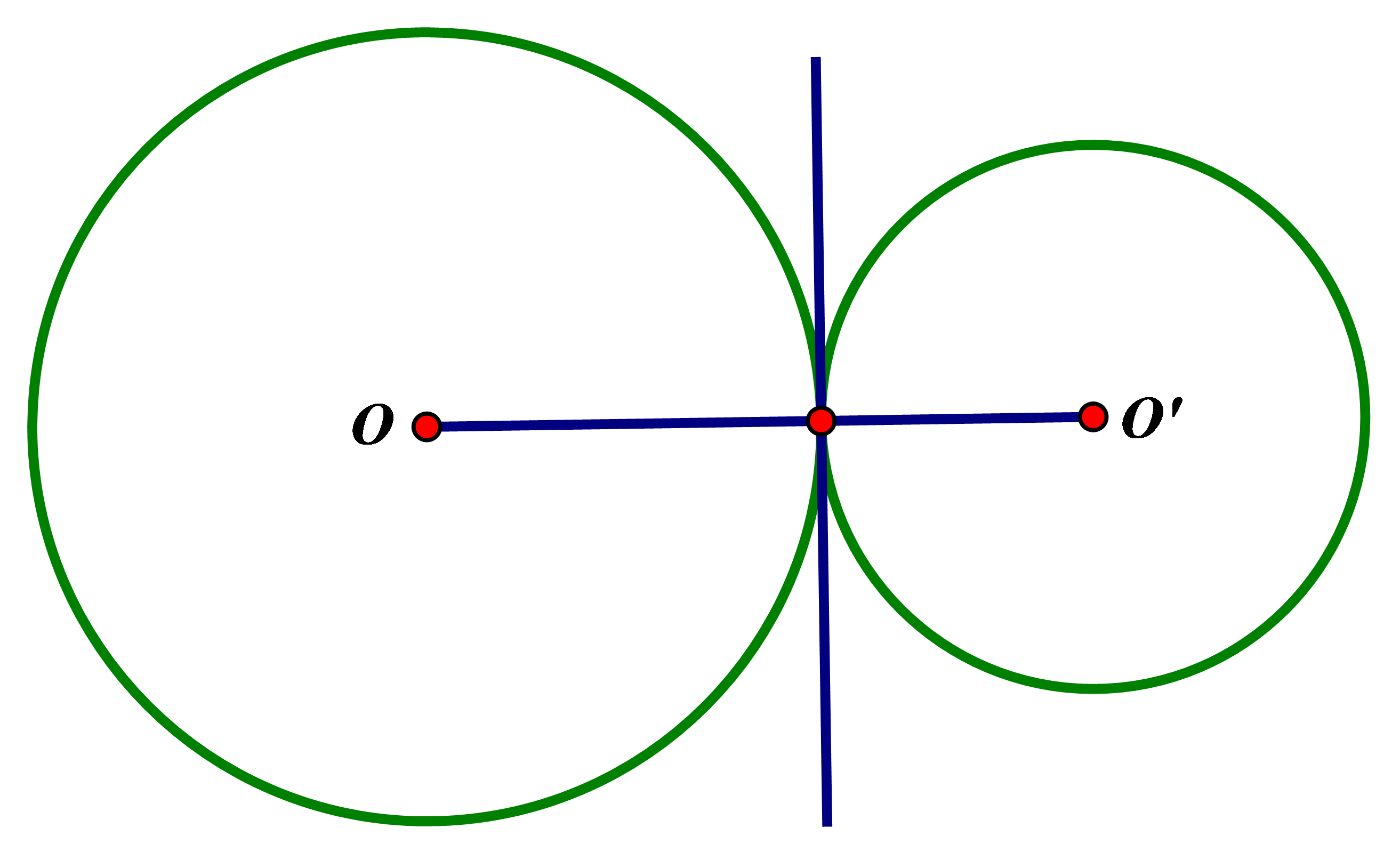
Tiếp tuyến chung của 2 đường tròn là đường thẳng tiếp xúc với cả 2 đường tròn đó. Ta có 1 số trường hợp tiếp tuyến chung như hình vẽ
Bài tập tự luyện có đáp án
Câu 1: Cho nửa đường tròn (O) , đường kính AB . Vẽ nửa đường tròn tâm O′ đường kính AO (cùng phía với nửa đường tròn (O) ). Một cát tuyến bất kỳ qua A cắt (O′);(O) lần lượt tại C,D . Nếu BC là tiếp tuyến của nửa đường tròn (O′) thì BC biểu diễn theo R (với OA=R ) có biểu thức là
- A
- B
- C
- D
Ta có OB=R;OO′=R2⇒O′B=3R2;O′C=R2
Theo định lý Pytago ta có: BC=√OB2−O′C2=√9R24−R24=√2R .
Câu 2: Cho đoạn OO′ và điểm A nằm trên đoạn OO′ sao cho OA=2O′A . Đường tròn (O) bán kính OA và đường tròn (O′) bán kính O′A . Vị trí tương đối của hai đường tròn là
- A
- B
- C
- D
Vì hai đường tròn có một điểm chung là A và OO′=OA+O′A=R+r nên hai đường tròn tiếp xúc ngoài.
Câu 3: Cho hai đường tròn (O;R) và (O′;R′) (R>R′) tiếp xúc ngoài tại A . Vẽ các bán kính OB//O′D với B,D ở cùng phía nửa mặt phẳng bờ OO′ . Đường thẳng DB và OO′ cắt nhau tại I . Tiếp tuyến chung ngoài GH của (O) và (O′) với G,H nằm ở nửa mặt phẳng bờ OO′ không chứa B,D . Tính OI theo R và R′ .
- A
- B
- C
- D
Xét tam giác IOB có OB//O′D (gt)
Áp dụng định lí Ta-let ta có OIO′I=OBO′D⇔OIO′I=RR′ mà O′I=OI−OO′=OI−(OA+AO′)=OI−(R+R′)
Nên OIOI−(R+R′)=RR′⇒OI.R′=R[OI−(R+R′)]⇔OI.R−OI.R′=R(R+R′) .
⇔OI(R−R′)=R(R+R′)⇔OI=R(R+R′)R−R′ .
Câu 4: Cho hai đường tròn (O);(O′) cắt nhau tại A,B trong đó O′∈(O) . Kẻ đường kính O′OC của đường tròn (O) . Khẳng định sai là :
- A
- B
- C
- D
Xét đường tròn (O) có O′C là đường kính, suy ra ^CBO′=^CAO′=90∘ hay CB⊥O′B tại B và AC⊥AO′ tại A .
Do đó AC,BC là hai tiếp tuyến của (O′) nên AC=CB (tính chất hai tiếp tuyến cắt nhau).
Câu 5: Cho đoạn OO′ và điểm A nằm trên đoạn OO′ sao cho OA=2O′A . Đường tròn (O) bán kính OA và đường tròn (O′) bán kính O′A . Dây AD của đường tròn lớn cắt đường tròn nhỏ tại C . Khi đó
- A
- B
- C
- D
Xét đường tròn (O′) và (O) có O′A=12OA nên OAO′A=2 .
Xét ΔO′AC cân tại O′ và ΔOAD cân tại O , có ^OAD=^O′AC (đối đỉnh) nên ^ODA=^O′CA
Suy ra ΔOAD ∽ ΔO′AC (g - g) ⇒ADAC=OAO′A=2
Lại có vì ^OAD=^O′CA mà hai góc ở vị trí so le trong nên OD//O′C .
Câu 6: Cho hai đường tròn (O;20cm) và (O′;15cm) cắt nhau tại A và B . Biết rằng AB=24cm và O và O′ nằm cùng phía đối với AB . Đoạn nối tâm OO′ có độ dài bằng
- A
- B
- C
- D
Ta có AI=12AB=12cm .
Theo định lý Pytago ta có:
OI2=OA2−AI2=256⇒OI=16cm
O′I=√O′A2−IA2=9cm
Do đó: OO′=OI−O′I=16−9=7(cm) .
Câu 7: Cho hai đường tròn (O;6cm) và (O′;2cm) cắt nhau tại A,B sao cho OA là tiếp tuyến của (O′) . Độ dài dây AB là
- A
- B
- C
- D
Vì OA là tiếp tuyến của (O′) nên ΔOAO′ vuông tại A .
Vì (O) và (O′) cắt nhau tại A,B nên đường nối tâm OO′ là trung trực của đoạn AB .
Gọi giao điểm của AB và OO′ là I thì AB⊥OO′ tại I là trung điểm của AB .
Áp dụng hệ thức lượng trong tam giác OAO′ ta có
1AI2=1OA2+1O′A2=162+122⇒AI=3√105cm⇒AB=6√105cm .
Câu 8: Cho hai đường tròn (O;8cm) và (O′;6cm) cắt nhau tại A,B sao cho OA là tiếp tuyến của (O′) . Độ dài dây AB là?
- A
- B
- C
- D

Vì OA là tiếp tuyến của (O′) nên ΔOAO′ vuông tại A .
Vì (O),(O′) cắt nhau tại A,B nên đường nối tâm OO′ là trung trực của đoạn AB
Gọi giao điểm của AB và OO′ là I thì AB⊥OO ′ tại I là trung điểm của AB
Áp dụng hệ thức lượng trong tam giác vuông OAO′ ta có
1AI2=1OA2+1O′A2=182+162⇒AI=4,8cm⇒AB=9,6cm
Câu 9: Cho hai đường tròn (O;R) và (O′;r) với R>r cắt nhau tại hai điểm phân biệt và OO′=d . Chọn khẳng định đúng?
- A
- B
- C
- D

Hai đường tròn (O;R) và (O′;r) với R>r cắt nhau,
Khi đó (O);(O′) có hai điểm chung và đường nối tâm là đường trung trực của đoạn AB .
Hệ thức liên hệ R−r<OO′<R+r
Câu 10: Cho hai đường tròn (O);(O′) tiếp xúc ngoài tại A . Kẻ tiếp tuyến chung ngoài MN với M∈(O);N∈(O′) . Gọi P là điểm đối xứng với M qua OO′;Q là điểm đối xứng với N qua OO′ . Khi đó MN+PQ bằng
- A
- B
- C
- D
Kẻ tiếp tuyến chung tại A của (O);(O′) cắt MN;PQ lần lượt tại B;C
Ta có MNPQ là hình thang cân nên ^NMP=^QPM
Tam giác OMP cân tại O nên ^OMP=^OPM suy ra
^OMP+^PMN=^OPM+^MPQ⇒^QPO=90∘
⇒OP⊥PQ tại P∈(O) nên PQ là tiếp tuyến của (O) .
Chứng minh tương tự ta có PQ là tiếp tuyến của (O′) .
Theo tính chất hai tiếp tuyến cắt nhau ta có: BA=BM=BN;CP=CA=CQ suy ra B;C lần lượt là trung điểm của MN;PQ và MN+PQ=2MB+2PC=2AB+2AC=2BC .
Lại có BC là đường trung bình của hình thang MNQP nên MP+NQ=2BC .
Do đó MN+PQ=MP+NQ .
Câu 11: Cho đoạn OO′ và điểm A nằm trên đoạn OO′ sao cho OA=2O′A . Đường tròn (O) bán kính OA và đường tròn (O′) bán kính O′A . Vị trí tương đối của hai đường tròn là
- A
- B
- C
- D
Vì hai đường tròn có một điểm chung là A và OO′=OA+O′A=R+r nên hai đường tròn tiếp xúc ngoài.
Câu 12: Cho đường tròn (O) bán kính OA và đường tròn (O′) đường kính OA .
Vị trí tương đối của hai đường tròn là
- A
- B
- C
- D

Vì hai đường tròn có một điểm chung là A và OO′=OA−OA2=R−r nên hai đường tròn tiếp xúc trong.
Câu 13: Cho (O1;3cm) tiếp xúc ngoài với (O2;1cm) tại A . Vẽ hai bán kính O1B và O2C song song với nhau cùng thuộc nửa mặt phẳng bờ O1O2 . Gọi D là giao điểm của BC và O1O2 . Tính độ dài O1D
- A
- B
- C
- D
Vì ΔO1BD có O1B//O2C nên theo hệ quả định lý Ta-let ta có
O2DO1D=O2CO1B=13 suy ra O1O2O1D=23 .
Mà O1O2=O1A+O2A=3+1=4⇒O1D=32.O1O2=32.4=6cm .
Câu 14: Cho hai đường tròn (O;8cm) và (O′;6cm) cắt nhau tại A,B sao cho OA là tiếp tuyến của (O′) . Độ dài dây AB là
- A
- B
- C
- D
Vì OA là tiếp tuyến của (O′) nên ΔOAO′ vuông tại A .
Vì (O) và (O′) cắt nhau tại A,B nên đường nối tâm OO′ là trung trực của đoạn AB .
Gọi giao điểm của AB và OO′ là I thì AB⊥OO′ tại I là trung điểm của AB .
Áp dụng hệ thức lượng trong tam giác OAO′ ta có:
1AI2=1OA2+1O′A2=182+162⇒AI=4,8cm⇒AB=9,6cm .
Câu 15: Cho đường tròn (O) bán kính OA và đường tròn (O′) đường kính OA .
Dây AD của đường tròn lớn cắt đường tròn nhỏ tại C. Khi đó
- A
- B
- C
- D

Xét đường tròn (O′) có OA là đường kính và C∈(O′) nên ΔACO vuông tại C hay OC⊥AD
Xét đường tròn (O) có OA=OD ⇒ΔOAD cân tại O có OC là đường cao cũng là đường trung tuyến nên CD=CA .
Câu 16: Cho hai đường tròn (O;R) và (O′;R′) (R>R′) tiếp xúc ngoài tại A . Vẽ các bán kính OB//O′D với B,D ở cùng phía nửa mặt phẳng bờ OO′ . Đường thẳng DB và OO′ cắt nhau tại I . Tiếp tuyến chung ngoài GH của (O) và (O′) với G,H nằm ở nửa mặt phẳng bờ OO′ không chứa B,D . Chọn khẳng định đúng.
- A
- B
- C
- D
Gọi giao điểm của OO′ và GH là I′
Ta có OG//O′H (do cùng vuông góc GH )
Theo định lí Talet trong tam giác OGI′ ta có
I′OI′O′=OGO′H=RR′ hay I′OI′O′=OIO′I=RR′
⇒I′ trùng với I
Vậy BD,OO′ và GH đồng quy.
Câu 17: Cho hai đường tròn (O);(O′) cắt nhau tại A,B trong đó O′∈(O) . Kẻ đường kính O′OC của đường tròn (O) . Chọn khẳng định sai.
- A
- B
- C
- D
Xét đường tròn (O) có O′C là đường kính, suy ra ^CBO′=^CAO′=90∘ hay CB⊥O′B tại B và AC⊥AO′ tại A .
Do đó AC,BC là hai tiếp tuyến của (O′) nên AC=CB (tính chất hai tiếp tuyến cắt nhau)
Câu 18: Cho hai đường tròn (O);(O′) cắt nhau tại A,B . Kẻ đường kính AC của đường tròn (O) và đường kính AD của đường tròn (O′) . Khẳng định sai là
- A
- B
- C
- D
Hai đường tròn (O);(O′) cắt nhau tại A và B tại A và B nên OO′ là đường trung trực của AB
⇒OO′⊥AB (tính chất đường nối tâm) nên đáp án C đúng.
Xét đường tròn (O) có AC là đường kính, suy ra ΔABC vuông tại B hay ^CBA=90∘ .
Xét đường tròn (O) có AD là đường kính, suy ra ΔABD vuông tại B hay ^DBA=90∘ .
Suy ra ^CBA+^DBA=90∘+90∘=180∘ hay ba điểm B,C,D thẳng hàng nên đáp án B đúng.
Xét tam giác ADC có O là trung điểm đoạn AC và O′ là trung điểm đoạn AD nên OO′ là đường trung bình của tam giác ACD⇒OO′=DC2 (tính chất đường trung bình) .
Câu 19: Cho hai đường tròn (O;R) và (O′;r) với R>r cắt nhau tại hai điểm phân biệt và OO′=d . Chọn khẳng định đúng.
- A
- B
- C
- D
Hai đường tròn (O;R) và (O′;r) (R>r) cắt nhau.
Khi đó (O) và (O′) có hai điểm chung và đường nối tâm là đường trung trực của đoạn AB .
Hệ thức liên hệ R−r<OO′<R+r .
Câu 20: Cho đường tròn (O) bán kính OA và đường tròn (O′) đường kính OA .Dây AD của đường tròn cắt đường tròn nhỏ tại C . Khi đó
- A
- B
- C
- D
Xét đường tròn (O′) có OA là đường kính và C∈(O′) nên ΔACO vuông tại C hay OC⊥AD .
Xét đường tròn (O) có OA=OD⇒ΔOAD cân tại O có OC là đường cao cũng là đường trung tuyến nên CD=CA .
Câu 21: Cho hai đường tròn (O);(O′) tiếp xúc ngoài tại A . Kẻ tiếp tuyến chung ngoài MN với M∈(O);N∈(O′) . Gọi P là điểm đối xứng với M qua OO′;Q là điểm đối xứng với N qua OO′ . Khi đó, tứ giác MNQP là hình gì?
- A
- B
- C
- D
Vì P là điểm đối xứng với M qua OO′
Q là điểm đối xứng với N qua OO′ nên MN=PQ .
P∈(O);Q∈(O′)
Mà MP⊥OO′;NQ⊥OO′
⇒MP//NQ mà MN=PQ
Nên MNPQ là hình thang cân.
Câu 22: Cho hai đường tròn (O;10cm) và (O′;5cm) cắt nhau tại A và B . Biết rằng AB=8cm và O và O′ nằm cùng phía đối với AB . Đoạn nối tâm OO′ có độ dài là : (làm tròn đến chữ số thập phân thứ nhất)
- A
- B
- C
- D
Ta có AI=12AB=4cm .
Theo định lý Pytago ta có:
OI2=OA2−AI2=102−42=84⇒OI=2√21cm
O′I=√O′A2−IA2=√52−42=3
Do đó: OO′=OI−O′I=2√21−3≈6,2(cm) .
Câu 23: Cho hai đường tròn (O1) và (O2) tiếp xúc ngoài tại A và một đường thẳng d tiếp xúc với (O1);(O2) lần lượt tại B,C . Tam giác ABC là
- A
- B
- C
- D
Xét (O1) có O1B=O1A
⇒ΔO1AB cân tại O1
⇒^O1BA=^O1AB
Xét (O2) có O2C=O2A
⇒ΔO2CA cân tại O2
⇒^O2CA=^O2AC
Mà ^O1+^O2=360∘−ˆC−ˆB=180∘
⇔180∘−^O1BA−^O1AB+180∘−^O2CA−^O2AC=180∘
⇔2(^O1AB+^O2AC)=180∘
⇒^O1AB+^O2AC=90∘
⇒^BAC=90∘
⇒ΔABC vuông tại A .
Câu 24: Cho đường tròn (O) bán kính OA và đường tròn (O′) đường kính OA . Dây AD của đường tròn cắt đường tròn nhỏ tại C . Khi đó
- A
- B
- C
- D
Xét đường tròn (O′) có OA là đường kính và C∈(O′) nên ΔACO vuông tại C hay OC⊥AD .
Xét đường tròn (O) có OA=OD⇒ΔOAD cân tại O có OC là đường cao cũng là đường trung tuyến nên CD=CA .
Câu 25: Cho hai đường tròn (O) và (O′) tiếp xúc ngoài tại A . Kẻ các đường kính AOB;AO′C . Gọi DE là tiếp tuyến chung của hai đường tròn (D∈(O);E∈(O′)) . Gọi M là giao điểm của BD và CE . Tính diện tích tứ giác ADME biết ^DOA=60∘ và OA=6cm .
- A
- B
- C
- D
Dễ dàng chứng minh được ^DAE=90∘
Mà ^BDA=90∘ (vì tam giác BAD có cạnh AB là đường kính
của (O) và D∈(O) ) nên BD⊥AD⇒^MDA=90∘ .
Tương tự ta có ^MEA=90∘ .
Nên tứ giác DMEA là hình chữ nhật.
Xét tam giác OAD cân tại O có ^DOA=60∘ nên ΔDOA đều
Suy ra OA=AD=6cm và ^ODA=60∘ ⇒^ADE=30∘ .
Xét tam giác ADE ta có: EA=AD.tan^EDA=6.tan30∘=2√3
SDMEA=AD.AE=6.2√3=12√3cm2 .
Câu 26: Cho hai đường tròn (O;20cm) và (O′;15cm) cắt nhau tại A và B . Tính đoạn nối tâm OO′ , biết rằng AB=24cm và O và O′ nằm cùng phía đối với AB .
- A
- B
- C
- D
Ta có AI=12AB=12cm .
Theo định lý Pytago ta có
OI2=OA2−AI2=256⇒OI=16cm
O′I=√O′A2−IA2=9cm
Do đó: OO′=OI−O′I=16−9=7(cm) .
Câu 27: Cho nửa đường tròn (O) , đường kính AB . Vẽ nửa đường tròn tâm O′ đường kính AO (cùng phía với nửa đường tròn (O) ). Một cát tuyến bất kỳ qua A cắt (O′);(O) lần lượt tại C,D . Chọn khẳng định sai.
- A
- B
- C
- D
Xét đường tròn (O′) có OA là đường kính và C∈(O′) nên ^ACO=90∘⇒AD⊥CO
Xét đường tròn (O) có OA=OD⇒ΔOAD cân tại O có OC là đường cao nên OC cũng là đường trung tuyến hay C là trung điểm của AD .
Xét tam giác AOD có O′C là đường trung bình nên O′C//OD
Kẻ các tiếp tuyến Cx;Dy với các nửa đường tròn ta có Cx⊥O′C;Dy⊥OD mà O′C//OD nên Cx⊥Dy .
Câu 28: Cho hai đường tròn (O;10cm) và (O′;5cm) cắt nhau tại A và B . Tính đoạn nối tâm OO′ , biết rằng AB=8cm và O và O′ nằm cùng phía đối với AB . (làm tròn đến chữ số thập phân thứ nhất).
- A
- B
- C
- D
Ta có AI=12AB=4cm .
Theo định lý Pytago ta có:
OI2=OA2−AI2=102−42=84⇒OI=2√21cm
O′I=√O′A2−IA2=√52−42=3
Do đó: OO′=OI−O′I=2√21−3≈6,2(cm) .
Câu 29: Cho các đường tròn (A;10cm),(B;15cm),(C;15cm) tiếp xúc ngoài với nhau đôi một. Hai đường tròn (B) và (C) tiếp xúc với nhau tại A′ . Đường tròn (A) tiếp xúc với đường tròn (A) và (B) lần lượt tại C′ và B′ . Chọn khẳng định đúng.
- A
- B
- C
- D
+ Theo tính chất đoạn nối tâm của hai đường tròn tiếp xúc ngoài ta có:
AB=BC′+C′A=25cm;AC=AB′+B′C=25cm;BC=BA′+A′C=30cm và A′ là trung điểm của BC (vì A′B=A′C=15cm )
ΔABC cân tại A có AA′ là đường trung tuyến nên cũng là đường cao
⇒AA′⊥BC
⇒AA′ là tiếp tuyến chung của hai đường tròn (B) và (C)
Xét tam giác AA′C vuông tại A′ ta có A′A2=AC2−A′C2=252−152=400⇒A′A=20cm
Câu 30: Cho hai đường tròn (O);(O′) cắt nhau tại A,B . Kẻ đường kính AC của đường tròn (O) và đường kính AD của đường tròn (O′) . Chọn khẳng định sai.
- A
- B
- C
- D
Hai đường tròn (O);(O′) cắt nhau tại A và B tại A và B nên OO′ là đường trung trực của AB ⇒OO′⊥AB (tính chất đường nối tâm).
Xét đường tròn (O) có AC là đường kính, suy ra ΔABC vuông tại B hay ^CBA=90∘ .
Xét đường tròn (O) có AD là đường kính, suy ra ΔABD vuông tại B hay ^DBA=90∘ .
Suy ra ^CBA+^DBA=90∘+90∘=180∘ hay ba điểm B,C,D thẳng hàng.
Xét tam giác ADC có O là trung điểm đoạn AC và O′ là trung điểm đoạn AD nên OO′ là đường trung bình của tam giác ACD⇒OO′=DC2 (tính chất đường trung bình).
Ta chưa thể kết luận gì về độ dài BC và BD .
Câu 31: Cho hai đường tròn (O;8cm) và (O′;6cm) cắt nhau tại A,B sao cho OA là tiếp tuyến của (O′) . Độ dài dây AB là
- A
- B
- C
- D
Vì OA là tiếp tuyến của (O′) nên ΔOAO′ vuông tại A .
Vì (O) và (O′) cắt nhau tại A,B nên đường nối tâm OO′ là trung trực của đoạn AB .
Gọi giao điểm của AB và OO′ là I thì AB⊥OO′ tại I là trung điểm của AB .
Áp dụng hệ thức lượng trong tam giác OAO′ ta có
1AI2=1OA2+1O′A2=182+162⇒AI=4,8cm⇒AB=9,6cm .
Xem thêm các bài tiếp theo bên dưới