Khoảng cách từ một điểm tới một mặt phẳng, một đường thẳng
Lý thuyết về Khoảng cách từ một điểm tới một mặt phẳng, một đường thẳng
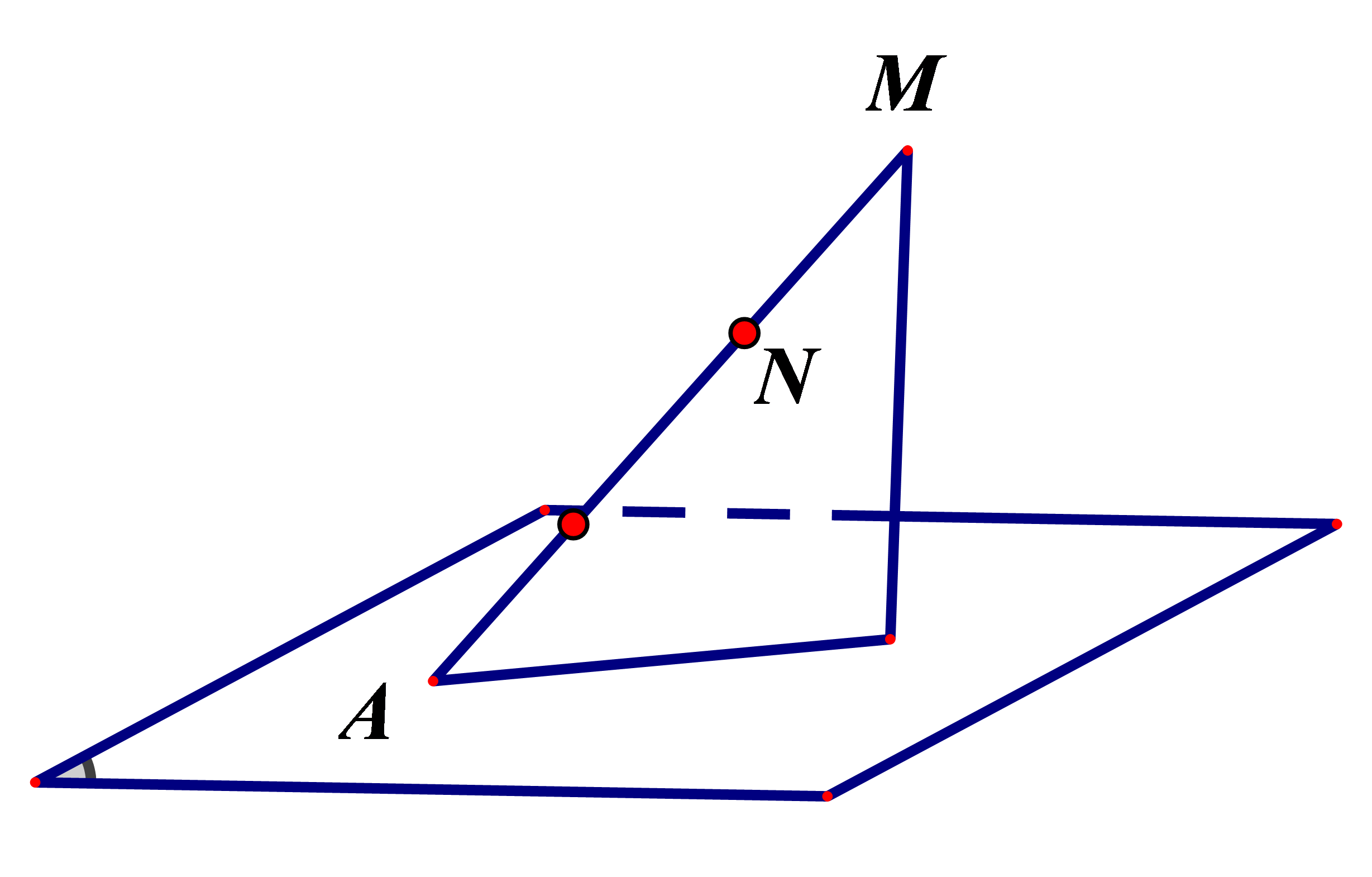
Phương pháp xác định khoảng cách từ điểm M đến mp(P)
Cách 1:
+ Tìm (Q)(Q)chứa M và vuông góc với (P)(P) theo giao tuyến ΔΔ
+ Từ M hạ MH vuông góc với ∆ (H∈ΔH∈Δ)
+ MH=d(M,(P))MH=d(M,(P))
Cách 2:
+ Kẻ Δ//(P)Δ//(P) . Ta có: d(M,(P))=d(Δ,(P))d(M,(P))=d(Δ,(P))
+ Chọn N∈ΔN∈Δ. Lúc đó, d(M,(P))=d(Δ,(P))=d(N,(P))d(M,(P))=d(Δ,(P))=d(N,(P))
Cách 3:
+ Nếu MN∩(P)=IMN∩(P)=I. Ta có: d(M,(P))d(N,(P))=MINId(M,(P))d(N,(P))=MINI
+ Tính d(N,(P))d(N,(P)) và MINIMINI
+ d(M,(P))=MINI.d(N,(P))d(M,(P))=MINI.d(N,(P))
Chú ý: Điểm NNở đây ta phải chọn sao cho tìm khoảng cách từ N đến mặt phẳng (P)(P) dễ hơn tìm khoảng cách từ MMđến (P).(P).
Bài tập tự luyện có đáp án
Câu 1: Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Trong các khẳng định sau, khẳng định nào là khẳng định đúng?
- A
- B
- C
- D
Câu 2: Cho mặt phẳng (P) và điểm M ngoài(P), khoảng cách từ M đến (P) bằng 6. Lấy A thuộc (P) và N trên AM sao cho 2MN=NA. Khoảng cách từ N đến (P) bằng bao nhiêu?
- A
- B
- C
- D

ANAM=d(N,(P))d(M,(P))⇒d(N(P))=23.6=4
Câu 3: Cho hình lập phương ABCD.A′B′C′D′cạnha. Khoảng cách từ C đến AC′ là:
- A
- B
- C
- D

d(C;AC′)=CK,CK⊥AC′ tại K
1CK2=1AC2+1CC′2=1(a√2)2+1a2=32a2 ⇒CK=a√63
Câu 4: Cho hình chóp tam giác đều S.ABC cạnh đáy bằng 2a và chiều cao bằng a√3. Tính khoảng cách từ tâm O của đáy ABC đến một mặt bên:
- A
- B
- C
- D

Gọi M là trung điểm AB,dựng OK⊥SM.d(O;(SAB))=OK
1OK2=1OM2+1SO2=1(a√33)2+1(a√3)2 ⇒OK=a√310
Câu 5: Trong các mệnh đề sau mệnh đề nào là sai?
Cho tứ diện đềuABCD. Khoảng cách từ điểm D tới mặt phẳng (ABC) là:
- A
- B
- C
- D
Chọn đáp án B.
Câu 6: Cho hình hôp chữ nhật ABCD.A′B′C′D′ có AB=AA′=a, AC=2a. Khoảng cách từ điểm D đến mặt phẳng(ACD′) là:
- A
- B
- C
- D

Dựng DH⊥AC,DK⊥D′H .d(D,(ACD′))=DK, 1DK2=1DD′2+1DA2+1DC2=73a2⇒DK=a√217
Câu 7: Cho hình hộp chữ nhật ABCD.A′B′C′D′có AB=a,BC=b,CC′=c. Khoảng cách từ B đến mặt phẳng (ACC′A′) là:
- A
- B
- C
- D

Dựng BH⊥AC. d(BB′,AC′)=d(B,(A′ACC′))=BH=BA.BCAC=a.b√a2+b2
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và AB=2a,BC=a. Các cạnh bên của hình chóp bằng nhau và bằng a√2. Tính khoảng cách h từ S đến mặt phẳng đáy (ABCD).
- A
- B
- C
- D
Hình chiếu của S lên mặt phẳng đáy là tâm đường tròn ngoại tiếp của đáy do hình chóp có các cạnh bên bằng nhau.
Mà đáy là hình chữ nhật nên tâm đường tròn ngoại tiếp chính là tâm của hình chữ nhật, hay là giao điểm O của hai đường chéo.
Khi đó: h=SO=√SA2−OA2=√2a2−5a24=a√32
Câu 9: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng a√2. Tính khoảng cách từ tâm O của đáy ABCD đến một mặt bên:
- A
- B
- C
- D

Gọi M là trung điểm CD, OK⊥SM Khi đód(O,(SCD))=OK.
Ta có1OK2=1SO2+1OM2⇒OK=√23a
Câu 10: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Khoảng cách từ S đến mặt phẳng (ABC) bằng:
- A
- B
- C
- D

Gọi G là trọng tâm tam giác ABC . Do S.ABC là chóp đều nên SG⊥(ABC).
AM=3a√32⇒AG=23AM=a√3.
ΔSAG vuông tại SG=√SA2−AG2=√4a2−3a2=a.
Câu 11: Cho hình chóp S.ABC có SA⊥(ABC) , tam giác ABC đều cạnh a. Khoảng cách từ B đến mặt phẳng (SAC) bằng:
- A
- B
- C
- D

⇒BH⊥(SAC)⇒d(B,(SAC))=BH=a√32 (vì BH là đường cao trong ΔABC đều)
Câu 12: Cho hình chóp tam giác S.ABC với SA vuông góc với (ABC) và SA = 3a. Diện tích tam giác ABC bằng 2a2,BC=a. Khoảng cách từ S đến BC bằng bao nhiêu?
- A
- B
- C
- D

Kẻ AH vuông góc với BC:SΔABC=12AH.BC→AH=2.SΔABCBC=4a2a=4a
Khoảng cách từ S đến BC chính là SH
Dựa vào tam giác vuông ΔSAH ta có SH=√SA2+AH2=√(3a)2+(4a)2=5a
Câu 13: Hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 3a. Tính khoảng cách h từ đỉnh S tới mặt phẳng đáy.
- A
- B
- C
- D
Gọi H là hình chiếu của S lên (ABC), khi đó h=SH.
Do hình chóp S.ABC đều nên H là tâm của tam giác đều ABC. Suy ra HA=233a√32=a√3
⇒SH=√SA2−AH2=a√6
Câu 14: Cho hình chóp S.ABCDcó đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy, SA=a. Gọi M là trung điểm của CD . Khoảng cách từ M đến (SAB) nhận giá trị nào trong các giá trị sau?
- A
- B
- C
- D
Khoảng cách từ M đến (SAB): d(M,(SAB))=d(D,(SAB))=a.
Câu 15: Cho hình chóp S.ABC trong đóSA, AB, BC vuông góc với nhau từng đôi một. Biết SA=3a, AB=a√3,BC=a√6. Khoảng cách từ B đến SC bằng:
- A
- B
- C
- D
SA⊥(ABC),ΔSBC vuông tại B; BH⊥SC tại H
⇒d(B,SC)=BH
Ta có: BH.SC=SB.BC; SC=3√2a,SB=2√3a, suy ra BH=2a.
Câu 16: Chỉ ra khẳng định không đúng trong các khẳng định sau
- A
- B
- C
- D
Khi hai đường thẳng vuông góc với nhau và chéo nhau thì sẽ không có đường vuông góc chung.
Câu 17: Cho hình chóp S.ABCD có SA⊥( ABCD) đáy ABCDlà hình thoi cạnh bằng a và ˆB=600. Biết SA=2a. Khoảng cách từ A đến SC là:
- A
- B
- C
- D

ΔABC đều,AC=a. Dựng AK⊥SC,AK=d(A;SC).
1AK2=1SA2+1AC2=1(2a)2+1a2=54a2⇒AK=2a√55
Câu 18: Cho lăng trụ ABC.A′B′C′ có SABC bằng a22 và thể tích bằng a3√34 . Khoảng cách từ A′ đến mặt phẳng (ABC) bằng
- A
- B
- C
- D
Ta có VABC.A′B′C′=d(A′;(ABC)).SABC⇒d(A′;(ABC))=a√32.
Câu 19: Chỉ ra khẳng định sai trong các khẳng định sau:
- A
- B
- C
- D
Khoảng cách từ một điểm đến một mặt phẳng là khoảng cách từ điểm đó tới mặt phẳng.